Machine Learning Notes: GNN, GraphNeT
§1 Graph
A graph is a data structure that has the shape $\mathbb{R} ^{N \times P}$, where
- $N$ is the number of nodes. Note that $N$ might vary in a dataset, but we often use cutting or padding to get a uniform, normalized $N$.
- $P$ is the number of features. Yes, the concept of “features” is similar to the concept of “channels” in CNNs.
A picture $\mathbb{R}^{H \times W \times C}$ is of height $H$ and width $W$, thus the total number of pixels is $HW$, and each pixel has $C$ channels, commonly $C=1$ (grey channel) or $C=3$ (RGB channels). Now let’s transform this picture into a graph $\mathbb{R}^{N \times P}$, where $N=HW$ is the total number of pixels. Thus $P=C+2$, which means the original position information is now encoded into the channels. What’s more, graph can represent more than that, thus in a sense, a graph is a generalized picture.
§1.1 Graph & Matrix
Graphs can be represented by adjacency matrix, which can be normalized into Frobenius normal form, see Matrices and graphs - by Tivadar Danka - The Palindrome.
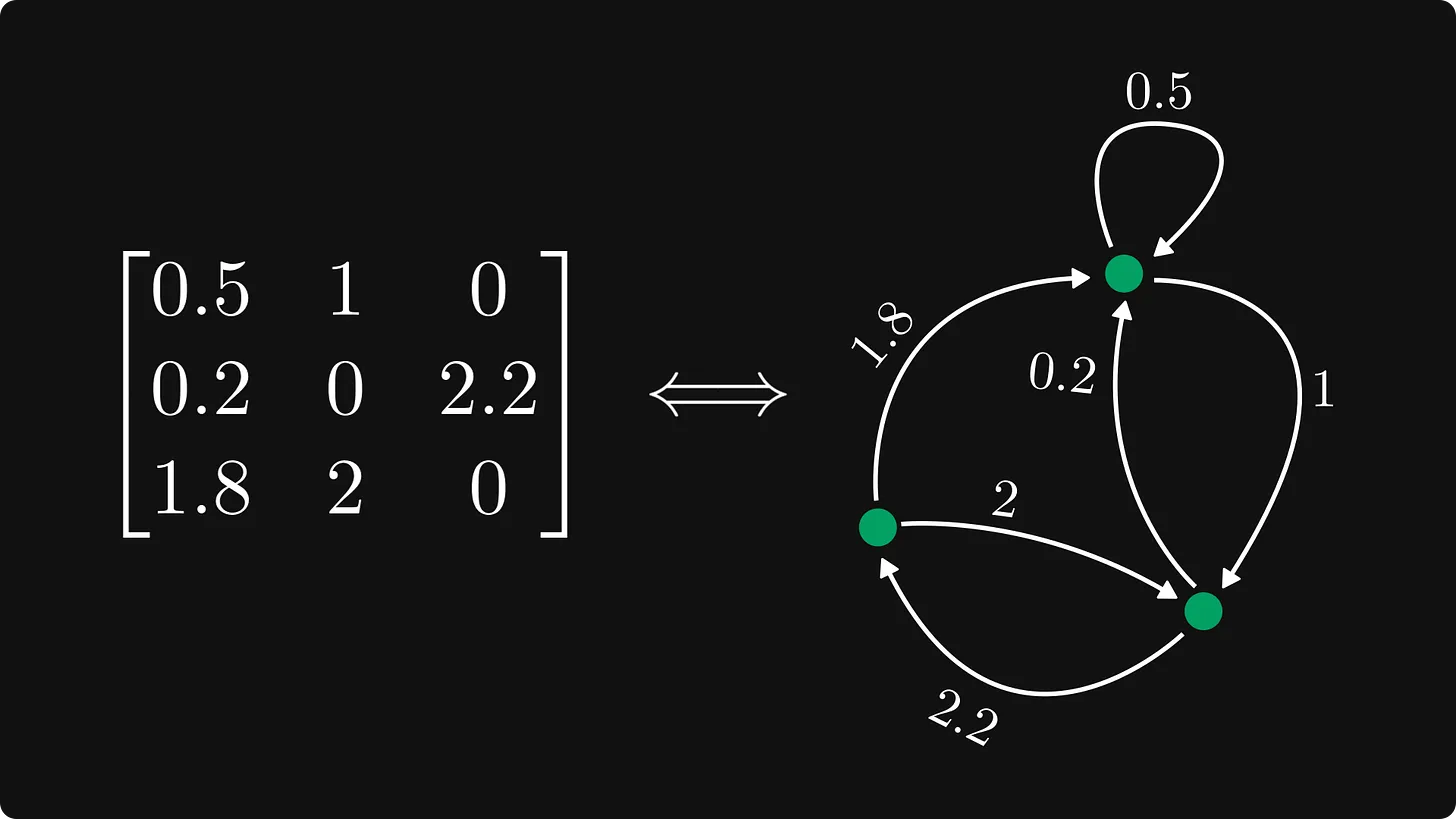
Often, large part of the matrix is empty, which is called Sparse matrix.
§2 GNN (PyTorch Geometric Style)
See A Gentle Introduction to Graph Neural Networks - Distill.pub. The general idea is that after GNN, part of the nodes are highlighted and the number of features of each nodes can be different. This is in consistence with CNN, where parts of the picture is highlighted and the number of channels (RGB $\rightarrow$ many more) can be different (see CNN Explainer).
Considering the popularity of LLMs, unsurprisingly, GNNs support Attention. For Graph Attention Networks (GAT), see Graph Attention Networks (GAT) (labml.ai) and Graph Attention Networks v2 (GATv2) (labml.ai).
This section is a skinner implementation of PyTorch Geometric from scratch, which means it’s NOT necessary to install the package, but I still recommend to do so for comparison:
pip install torch_geometric
And we import PyTorch as before:
import torch
import torch.nn as nn
import torch.nn.functional as F
§2.1 torch_geometric.utils
§2.1.1 add_self_loops
torch_geometric.utils.add_self_loopstorch_geometric.utils.add_self_loopsis pretty self-explaining.from torch_geometric.utils import add_self_loops def test_add_self_loops(): x = torch.rand((10, 16))# [num_nodes, in_channels] edge_index = torch.randint(0, 10, size=(2, 7))# [2, num_messages] edge_index, _ = add_self_loops(edge_index, num_nodes=x.shape[-2]) print(edge_index) print(edge_index.shape) test_add_self_loops()will get (note we get self loops here):
tensor([[4, 9, 7, 9, 3, 6, 9, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9], [5, 7, 4, 2, 7, 1, 2, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9]]) torch.Size([2, 17])my_add_self_loopsdef my_add_self_loops(edge_index, num_nodes): self_loops = torch.arange(num_nodes) if edge_index.dim() == 2: self_loops = self_loops.repeat(2, 1) elif edge_index.dim() == 3: batch_size = edge_index.shape[0] self_loops = self_loops.repeat(batch_size, 2, 1) else: raise RuntimeError(f'The dimension of edge_index should be 2 or 3. Got: {edge_index.dim()}') edge_index = torch.cat((edge_index, self_loops), dim=-1) edge_weight = None return edge_index, edge_weight def test_add_self_loops(): x = torch.rand((10, 16))# [num_nodes, in_channels] edge_index = torch.randint(0, 10, size=(2, 7))# [2, num_messages] edge_index, _ = my_add_self_loops(edge_index, num_nodes=x.shape[-2]) print(edge_index) print(edge_index.shape) x = torch.rand((3, 10, 16))# [batch_size, num_nodes, in_channels] edge_index = torch.randint(0, 10, size=(3, 2, 7))# [batch_size, 2, num_messages] edge_index, _ = my_add_self_loops(edge_index, num_nodes=x.shape[-2]) print(edge_index) print(edge_index.shape) test_add_self_loops()will get:
tensor([[0, 5, 2, 7, 8, 8, 5, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9], [0, 2, 6, 6, 9, 6, 3, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9]]) torch.Size([2, 17]) tensor([[[5, 7, 2, 4, 9, 8, 1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9], [5, 3, 3, 7, 0, 1, 9, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9]], [[9, 0, 4, 7, 4, 9, 1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9], [6, 2, 9, 7, 7, 4, 6, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9]], [[4, 5, 4, 2, 0, 3, 9, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9], [1, 9, 7, 4, 9, 4, 5, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9]]]) torch.Size([3, 2, 17])
§2.1.2 scatter
torch_geometric.utils.scatter is the same as Aggregation Operators. Below is the image from Scatter — pytorch_scatter 2.1.1 documentation:
torch_geometric.utils.scatterfrom torch_geometric.utils import scatter def test_scatter(): x = torch.rand((5, 8))# [num_index, in_channels] print(x) index = torch.randint(0, 5, size=(5,))# [num_index,] print(index) x = scatter(x, index, dim=-2, dim_size=10, reduce='sum')# [dim_size, in_channels] print(x) test_scatter()will get:
tensor([[0.0101, 0.3919, 0.6275, 0.1619, 0.2756, 0.9814, 0.5278, 0.9113], [0.1170, 0.4807, 0.8374, 0.6121, 0.1399, 0.3740, 0.4485, 0.0578], [0.7961, 0.2162, 0.8050, 0.2520, 0.2318, 0.0279, 0.9750, 0.3881], [0.2107, 0.2072, 0.8769, 0.7675, 0.2437, 0.6953, 0.2572, 0.4149], [0.6781, 0.9938, 0.4502, 0.1818, 0.2886, 0.2952, 0.1135, 0.9759]]) tensor([3, 0, 3, 1, 1]) tensor([[0.1170, 0.4807, 0.8374, 0.6121, 0.1399, 0.3740, 0.4485, 0.0578], [0.8888, 1.2010, 1.3271, 0.9493, 0.5323, 0.9904, 0.3706, 1.3908], [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000], [0.8061, 0.6080, 1.4325, 0.4139, 0.5074, 1.0093, 1.5027, 1.2994], [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000], [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000], [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000], [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000], [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000], [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000]])my_scatterdef my_scatter(input, index, dim_size, reduce='sum'): if input.dim() == 2:# [num_index, in_channels] num_index, in_channels = input.shape output = torch.zeros(dim_size, in_channels) # if reduce == 'sum': # for i in range(num_index): # output[index[i]] += input[i] index = index.unsqueeze(-1).expand(-1, in_channels) # https://pytorch.org/docs/stable/generated/torch.Tensor.scatter_reduce_.html output = output.scatter_reduce_(0, index, input, reduce=reduce)# [dim_size, in_channels] elif input.dim() == 3:# [batch_size, num_index, in_channels] batch_size, num_index, in_channels = input.shape output = torch.zeros(batch_size, dim_size, in_channels) index = index.unsqueeze(-1).expand(-1, -1, in_channels) output = output.scatter_reduce_(1, index, input, reduce=reduce)# [batch_size, dim_size, in_channels] else: raise RuntimeError(f'The dimension of input should be 2 or 3. Got: {input.dim()}') return output def test_scatter(): x = torch.rand((5, 8))# [num_index, in_channels] print(x) index = torch.randint(0, 5, size=(5,))# [num_index,] print(index) y1 = scatter(x, index, dim=-2, dim_size=10, reduce='sum')# [dim_size, in_channels] print(y1) y2 = my_scatter(x, index, dim_size=10, reduce='sum')# [dim_size, in_channels] print(y2) print(torch.all(y1==y2)) x = torch.rand((3, 5, 8))# [batch_size, num_index, in_channels] print(x) index = torch.randint(0, 5, size=(3, 5))# [batch_size, num_index] print(index) x = my_scatter(x, index, dim_size=10, reduce='sum')# [batch_size, dim_size, in_channels] print(x) test_scatter()will get:
tensor([[0.2109, 0.7352, 0.5434, 0.3313, 0.4879, 0.1099, 0.9719, 0.5557], [0.2895, 0.3029, 0.7941, 0.9762, 0.9781, 0.0098, 0.0681, 0.1918], [0.9410, 0.4957, 0.7365, 0.7754, 0.3758, 0.8361, 0.3774, 0.7967], [0.3614, 0.5214, 0.1778, 0.3030, 0.4437, 0.0416, 0.2726, 0.3489], [0.9101, 0.3961, 0.2422, 0.6505, 0.8651, 0.4071, 0.2292, 0.7021]]) tensor([2, 1, 2, 4, 0]) tensor([[0.9101, 0.3961, 0.2422, 0.6505, 0.8651, 0.4071, 0.2292, 0.7021], [0.2895, 0.3029, 0.7941, 0.9762, 0.9781, 0.0098, 0.0681, 0.1918], [1.1520, 1.2309, 1.2798, 1.1066, 0.8637, 0.9460, 1.3493, 1.3524], [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000], [0.3614, 0.5214, 0.1778, 0.3030, 0.4437, 0.0416, 0.2726, 0.3489], [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000], [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000], [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000], [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000], [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000]]) tensor([[0.9101, 0.3961, 0.2422, 0.6505, 0.8651, 0.4071, 0.2292, 0.7021], [0.2895, 0.3029, 0.7941, 0.9762, 0.9781, 0.0098, 0.0681, 0.1918], [1.1520, 1.2309, 1.2798, 1.1066, 0.8637, 0.9460, 1.3493, 1.3524], [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000], [0.3614, 0.5214, 0.1778, 0.3030, 0.4437, 0.0416, 0.2726, 0.3489], [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000], [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000], [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000], [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000], [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000]]) tensor(True) tensor([[[0.8990, 0.4597, 0.7653, 0.6775, 0.3636, 0.4298, 0.3261, 0.9486], [0.0308, 0.8333, 0.0035, 0.3883, 0.8613, 0.2124, 0.4893, 0.1022], [0.3727, 0.3074, 0.8212, 0.8106, 0.0155, 0.6888, 0.7277, 0.7075], [0.7739, 0.0090, 0.2914, 0.3589, 0.1572, 0.0859, 0.1171, 0.6445], [0.0477, 0.5978, 0.1796, 0.8697, 0.8681, 0.3389, 0.8583, 0.2979]], [[0.4149, 0.0501, 0.1444, 0.3398, 0.8869, 0.3870, 0.7668, 0.9858], [0.4371, 0.0038, 0.9366, 0.7123, 0.5654, 0.9842, 0.3148, 0.0612], [0.3490, 0.4695, 0.7684, 0.2278, 0.1113, 0.5987, 0.1896, 0.7463], [0.9775, 0.8479, 0.6687, 0.1694, 0.2184, 0.3508, 0.8931, 0.6718], [0.9636, 0.9075, 0.9465, 0.2474, 0.2375, 0.7783, 0.7889, 0.4870]], [[0.0773, 0.0997, 0.9874, 0.8786, 0.8156, 0.3476, 0.5336, 0.7997], [0.7374, 0.0760, 0.2192, 0.4114, 0.4912, 0.9106, 0.7786, 0.3500], [0.2275, 0.8594, 0.7933, 0.2454, 0.1883, 0.9494, 0.1048, 0.1753], [0.2489, 0.6791, 0.8371, 0.2103, 0.7531, 0.4672, 0.4845, 0.8223], [0.8476, 0.1368, 0.2671, 0.2773, 0.9175, 0.1492, 0.9960, 0.9908]]]) tensor([[0, 4, 1, 2, 3], [2, 3, 0, 0, 1], [2, 1, 0, 2, 4]]) tensor([[[0.8990, 0.4597, 0.7653, 0.6775, 0.3636, 0.4298, 0.3261, 0.9486], [0.3727, 0.3074, 0.8212, 0.8106, 0.0155, 0.6888, 0.7277, 0.7075], [0.7739, 0.0090, 0.2914, 0.3589, 0.1572, 0.0859, 0.1171, 0.6445], [0.0477, 0.5978, 0.1796, 0.8697, 0.8681, 0.3389, 0.8583, 0.2979], [0.0308, 0.8333, 0.0035, 0.3883, 0.8613, 0.2124, 0.4893, 0.1022], [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000], [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000], [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000], [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000], [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000]], [[1.3265, 1.3174, 1.4372, 0.3971, 0.3298, 0.9495, 1.0827, 1.4180], [0.9636, 0.9075, 0.9465, 0.2474, 0.2375, 0.7783, 0.7889, 0.4870], [0.4149, 0.0501, 0.1444, 0.3398, 0.8869, 0.3870, 0.7668, 0.9858], [0.4371, 0.0038, 0.9366, 0.7123, 0.5654, 0.9842, 0.3148, 0.0612], [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000], [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000], [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000], [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000], [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000], [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000]], [[0.2275, 0.8594, 0.7933, 0.2454, 0.1883, 0.9494, 0.1048, 0.1753], [0.7374, 0.0760, 0.2192, 0.4114, 0.4912, 0.9106, 0.7786, 0.3500], [0.3263, 0.7788, 1.8245, 1.0889, 1.5687, 0.8148, 1.0181, 1.6220], [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000], [0.8476, 0.1368, 0.2671, 0.2773, 0.9175, 0.1492, 0.9960, 0.9908], [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000], [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000], [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000], [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000], [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000]]])
§2.1.3 knn_graph
torch_geometric.nn.pool.knn_graph. Euclidean distances is similar to Attention.
def my_knn_graph(x, k=3, loop=False, cosine=False, xyz=False):
if x.dim() == 2:# [num_nodes, in_channels]
x = x.unsqueeze(0)# [batch_size, num_nodes, in_channels]
squeeze_at_the_end = True
elif x.dim() == 3:# [batch_size, num_nodes, in_channels]
squeeze_at_the_end = False
else:
RuntimeError(f'The dimension of x should be 2 or 3. Got: {x.dim()}')
batch_size, num_nodes, _ = x.shape
# pick out [batch_size, num_nodes, 3]. In this case, 3 stands for x, y, z.
if xyz:
x = x[:, :, :3]# [batch_size, num_nodes, 3]
if cosine:# cosine distances
x_norm = x / torch.norm(x, dim=-1, keepdim=True)
similarities = x_norm @ x_norm.transpose(-2, -1)
distances = 1 - similarities# [batch_size, num_nodes, num_nodes]
else:# Euclidean distances
distances = torch.cdist(x, x)# [batch_size, num_nodes, num_nodes]
# if `True`, contain self loops
if not loop:
mask = torch.eye(num_nodes, dtype=torch.bool).unsqueeze(0)
distances.masked_fill_(mask, float('inf'))
# k neighbors
_, indices = distances.topk(k=k, dim=-1, largest=False)# [batch_size, num_nodes, k]
# concat, source to target
row = torch.arange(num_nodes).view(-1, 1).repeat(1, k).view(-1).repeat(batch_size, 1, 1)# [batch_size, 1, num_nodes * k]
col = indices.view(batch_size, -1).unsqueeze(-2)# [batch_size, 1, num_nodes * k]
edge_index = torch.cat([row, col], dim=-2) # [batch_size, 2, num_nodes * k]
if squeeze_at_the_end:
edge_index = edge_index.squeeze()
return edge_index
def test_knn_graph():
x = torch.rand(5, 8)# [num_nodes, in_channels]
edge_index = my_knn_graph(x)# [2, num_messages] = [2, num_nodes * k]
print(edge_index)
print(edge_index.shape)
x = torch.rand(3, 5, 8)# [batch_size, num_nodes, in_channels]
edge_index = my_knn_graph(x)# [batch_size, 2, num_messages] = [batch_size, 2, num_nodes * k]
print(edge_index)
print(edge_index.shape)
test_knn_graph()
will get:
tensor([[0, 0, 0, 1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4],
[2, 1, 4, 3, 2, 0, 1, 0, 3, 1, 2, 0, 0, 2, 1]])
torch.Size([2, 15])
tensor([[[0, 0, 0, 1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4],
[3, 1, 2, 2, 3, 0, 3, 1, 0, 2, 0, 4, 3, 2, 1]],
[[0, 0, 0, 1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4],
[3, 2, 4, 4, 3, 2, 3, 4, 1, 2, 4, 0, 2, 3, 1]],
[[0, 0, 0, 1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4],
[1, 3, 2, 0, 4, 2, 4, 3, 0, 4, 0, 2, 3, 2, 0]]])
torch.Size([3, 2, 15])
§2.2 torch_geometric.nn.conv
§2.2.1 MessagePassing
| Creating Message Passing Networks | torch_geometric.nn.conv.MessagePassing |
With $x_i \in R^F$ denoting node features of node $i$ and $e_{j, i} \in R^D$ denoting (optional) edge features from node $j$ to node $i$, message passing GNNs can be described as $$x_i^{\prime} = \gamma ( x_i, \bigoplus_{j \in \mathcal{N}(i)} , \phi (x_i, x_j,e_{j,i}) ),$$where
- $\phi$:
MessagePassing.message() - $\bigoplus$:
MessagePassing.aggregate() - $\gamma$:
MessagePassing.update()
Below is MyMessagePassing, later in this article TAGConv and EdgeConv are subclasses of this class.
class no_batch_MyMessagePassing(nn.Module):
def __init__(self, aggr='sum'):
super().__init__()
self.aggr = aggr
def message(self, x, edge_index):
row, col = edge_index# both [num_messages,]
x_i, x_j = x[row], x[col]# both [num_messages, in_channels]
return x_j
def aggregate(self, x_j, edge_index, num_nodes):
row, col = edge_index
x_j = my_scatter(x_j, col, dim_size=num_nodes, reduce=self.aggr)# [num_nodes, in_channels]
return x_j
def update(self, x_j):
return x_j
def propagate(self, x, edge_index=None):
num_nodes = x.shape[-2]
if edge_index is None:
edge_index = torch.zeros((2, 0), dtype=torch.int64)# [2, num_messages]
edge_index, _ = my_add_self_loops(edge_index, num_nodes=num_nodes)
x_j = self.message(x, edge_index)
x_j = self.aggregate(x_j, edge_index, num_nodes)
x_j = self.update(x_j)
return x_j
def forward(self, x, edge_index):
return self.propagate(x, edge_index)
class MyMessagePassing(nn.Module):
def __init__(self, aggr='sum'):
super().__init__()
self.aggr = aggr
def message(self, x, edge_index):
row, col = edge_index[:, 0, :], edge_index[:, 1, :]# both [batch_size, num_messages]
# torch do not support `x_i = x[row]` in this case, so here's the alternative:
x_i = torch.gather(x, 1, row.unsqueeze(-1).expand(-1, -1, x.shape[-1]))# [batch_size, num_messages, in_channels]
x_j = torch.gather(x, 1, col.unsqueeze(-1).expand(-1, -1, x.shape[-1]))# [batch_size, num_messages, in_channels]
return x_j
def aggregate(self, x_j, edge_index, num_nodes):
row, col = edge_index[:, 0, :], edge_index[:, 1, :]# both [batch_size, num_messages]
x_j = my_scatter(x_j, col, dim_size=num_nodes, reduce=self.aggr)# [batch_size, num_nodes, in_channels]
return x_j
def update(self, x_j):
return x_j
def propagate(self, x, edge_index=None):
batch_size, num_nodes, _ = x.shape
if edge_index is None:
edge_index = torch.zeros((batch_size, 2, 0), dtype=torch.int64)# [batch_size, 2, num_messages]
edge_index, _ = my_add_self_loops(edge_index, num_nodes=num_nodes)
x_j = self.message(x, edge_index)
x_j = self.aggregate(x_j, edge_index, num_nodes)
x_j = self.update(x_j)
return x_j
def forward(self, x, edge_index):
return self.propagate(x, edge_index)
§2.2.2 TAGConv
torch_geometric.nn.conv.TAGConv
TAGConv is defined as $$X^{\prime} = \sum_{k=0}^K \left( D^{-1/2} A D^{-1/2} \right)^k X W_k,$$where $A$ denotes the adjacency matrix and $D_{ii} = \sum_{j=0} A_{ij}$ its diagonal degree matrix.
class MyTAGConv(MyMessagePassing):
def __init__(self, in_channels, out_channels, K=4):
super().__init__()
self.linears = nn.ModuleList([
nn.Linear(in_channels, out_channels, bias=False)
for _ in range(K + 1)
])
self.bias = nn.Parameter(torch.empty(out_channels))
def forward(self, x, edge_index):
out = self.linears[0](x)
for linear in self.linears[1:]:
x_j = self.propagate(x, edge_index)
out = out + linear(x_j)
out = out + self.bias
return out
my_tag_conv = MyTAGConv(in_channels=16, out_channels=32)
x = torch.randn(3, 10, 16)# [batch_size, num_nodes, in_channels]
edge_index = my_knn_graph(x, k=3)# [batch_size, 2, num_nodes * k] = [batch_size, 2, num_messages]
x = my_tag_conv(x, edge_index)
print(x.shape)# [batch_size, num_nodes, out_channels]
will get:
torch.Size([3, 10, 32])
§2.2.3 EdgeConv
torch_geometric.nn.conv.EdgeConv
EdgeConv is defined as $$x_i^{\prime} = \sum_{j \in \mathcal{N}(i)} h_{\mathbf{\Theta}}(x_i , x_j - x_i)$$ where $h_{\mathbf{\Theta}}$ denotes a neural network.
class MyEdgeConv(MyMessagePassing):
def __init__(self, nn, aggr='max'):
super().__init__(aggr=aggr)
self.nn = nn
def message(self, x, edge_index):
row, col = edge_index[:, 0, :], edge_index[:, 1, :]# both [batch_size, num_messages]
# torch do not support `x_i = x[row]` in this case, so here's the alternative:
x_i = torch.gather(x, 1, row.unsqueeze(-1).expand(-1, -1, x.shape[-1]))# [batch_size, num_messages, in_channels]
x_j = torch.gather(x, 1, col.unsqueeze(-1).expand(-1, -1, x.shape[-1]))# [batch_size, num_messages, in_channels]
x_j = torch.cat([x_i, x_j - x_i], dim=-1)# [batch_size, num_nodes, 2 * in_channels]
x_j = self.nn(x_j)
return x_j
my_edge_conv = MyEdgeConv(
nn.Sequential(
nn.Linear(32, 64),# [2 * in_channels, hidden_channels]
nn.ReLU(),
nn.Linear(64, 128),# [hidden_channels, out_channels]
nn.ReLU()
)
)
x = torch.randn(3, 10, 16)# [batch_size, num_nodes, in_channels]
edge_index = my_knn_graph(x, k=3)# [batch_size, 2, num_nodes * k] = [batch_size, 2, num_messages]
x = my_edge_conv(x, edge_index)
print(x.shape)# [batch_size, num_nodes, out_channels]
will get:
torch.Size([3, 10, 128])
§3 GraphNeT
This section is a general introduction to GitHub repository GraphNeT. See their getting started document, especially the example. In the following article I will focus on the model rather than how to load the data or how to train the model with pytorch-lightning, and I will test these models with dummies. Because I just understand things better in this way and I haven’t used these models in practice.
§3.1 Shape of the Data
See 4. The Dataset and DataLoader classes of the getting started document:
graph.x: Node feature matrix with shape[num_nodes, num_features]graph.edge_index: Graph connectivity in COO format with shape[2, num_edges]and typetorch.long(by default this will beNone, i.e., the nodes will all be disconnected).
§3.2 graphnet.models.gnn
§3.2.1 ConvNet
graphnet.models.gnn.ConvNet is based on torch_geometric.nn.TAGConv. For the structure of the model, see Fig.3 of [2107.12187] Reconstruction of Neutrino Events in IceCube using Graph Neural Networks.

In [2107.12187], it’s stated that:
In the simplest way, each pulse can be described by following quantities: the hit DOM, and therefore the position of the pulse, collected charge, and time recorded. … We can then represent each event by a graph, with the nodes representing the pulses in an abstract 5-dimensional (or 12-dimensional for the Upgrade) space.
Therefore, the event is an input matrix in the shape of [number_of_pulses, 5], where 5 is x, y, z, time, charge.
§3.2.2 DynEdge
§3.2.2.1 DynEdgeConv
The basic layer of DynEdge is graphnet.models.components.layers.DynEdgeConv, which is based on torch_geometric.nn.EdgeConv.
§3.2.2.2 DynEdge
§3.2.2.3 DynEdgeJINST
graphnet.models.gnn.DynEdgeJINST is the model in Fig.2 of [2209.03042] Graph Neural Networks for Low-Energy Event Classification & Reconstruction in IceCube. [n, 6] in the figure means the number of nodes is n and the number of features is 6, while [1, n_outputs] means the prediction of this event has n_outputs features (azimuth, zenith, energy, etc.)

§3.2.2.4 DynEdgeTITO
From 1st Place Solution in the Kaggle Competition.
The structure of this model is as follows:
graphnet.models.gnn.DynEdgeTITOgraphnet.models.components.layers.DynTransgraphnet.models.components.layers.DynTransgraphnet.models.components.layers.EdgeConvTitotorch.nn.TransformerEncodertorch.nn.TransformerEncoderLayer
graphnet.models.components.layers.DynTransgraphnet.models.components.layers.EdgeConvTitotorch.nn.TransformerEncodertorch.nn.TransformerEncoderLayer
- Post-processing
- Global pooling
- Read-out
For torch.nn.TransformerEncoderLayer, d_model=256 and nhead=8, and by default dim_feedforward=2048.
One of the layers graphnet.models.components.layers.EdgeConvTito is a modification on torch_geometric.nn.EdgeConv (See §2.3.3): $$x_i^{\prime} = \sum_{j \in \mathcal{N}(i)} h_{\mathbf{\Theta}}(x_i , x_j - x_i , x_j)$$
Here we subclass MyMessagePassing to write it from scratch:
class MyEdgeConvTito(MyMessagePassing):
def __init__(self, nn, aggr='max'):
super().__init__(aggr=aggr)
self.nn = nn
def message(self, x, edge_index):
row, col = edge_index[:, 0, :], edge_index[:, 1, :]# both [batch_size, num_messages]
# torch do not support `x_i = x[row]` in this case, so here's the alternative:
x_i = torch.gather(x, 1, row.unsqueeze(-1).expand(-1, -1, x.shape[-1]))# [batch_size, num_messages, in_channels]
x_j = torch.gather(x, 1, col.unsqueeze(-1).expand(-1, -1, x.shape[-1]))# [batch_size, num_messages, in_channels]
x_j = torch.cat([x_i, x_j - x_i, x_j], dim=-1)# [batch_size, num_nodes, 3 * in_channels]
x_j = self.nn(x_j)
return x_j
my_edge_conv_tito = MyEdgeConvTito(
nn.Sequential(
nn.Linear(48, 64),# [3 * in_channels, hidden_channels]
nn.ReLU(),
nn.Linear(64, 128),# [hidden_channels, out_channels]
nn.ReLU()
)
)
x = torch.randn(3, 10, 16)# [batch_size, num_nodes, in_channels]
edge_index = my_knn_graph(x, k=3)# [batch_size, 2, num_nodes * k] = [batch_size, 2, num_messages]
x = my_edge_conv_tito(x, edge_index)
print(x.shape)# [batch_size, num_nodes, out_channels]
will get:
torch.Size([3, 10, 128])