Wow It Fits! — Secondhand Machine Learning
(There are a lot of pictures so it might take a while to load. This article is actually longer than it looks, because I use tabsets a lot.)
§1 Intro
This section is about tensor (high-dimensional matrix) and torch.nn.
§1.1 Tensor
In the rest of the article, we will always:
import torch
import torch.nn as nn
import torch.nn.functional as F
from torchinfo import summary
§1.1.1 Shape
e.g. [H, W, C] (usually used in numpy or matplotlib.pyplot) or [C, H, W] (usually used in torch) or [batch_size, C, H, W].
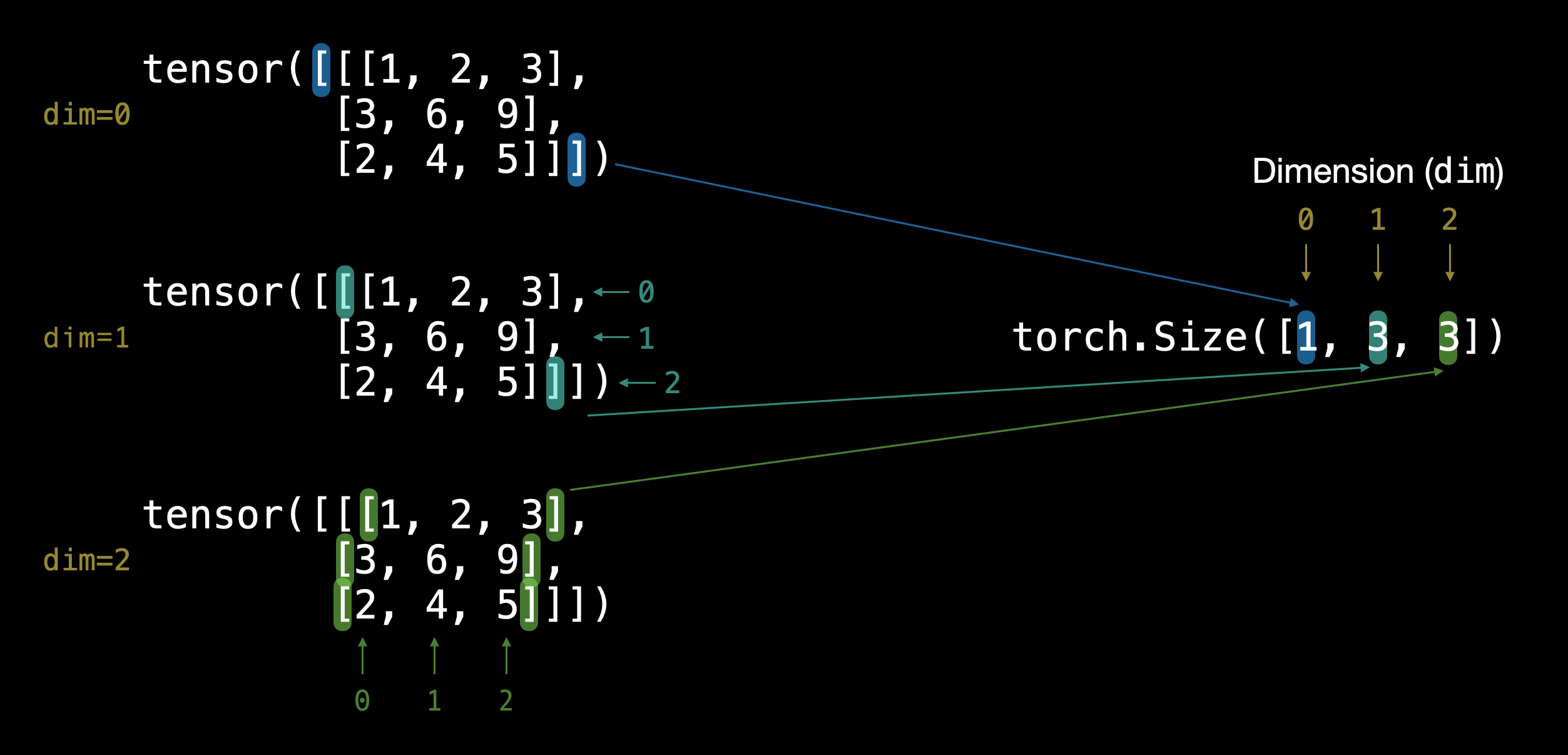
dummy = torch.randn(1, 3, 32, 32)# [batch_size, C, H, W]
print(dummy.shape)
will get:
torch.Size([1, 3, 32, 32])
Commonly used method to change the shape of a tensor:
.view().reshape()(.reshape()is for non-contiguous tensor, try.view()first.x.reshape()is equal tox.contiguous().view()).unsqueeze().squeeze().transpose().permute()
einops provides a more intuitive way to change the shape.
§1.1.2 Device
Tensor device
dummy = torch.randn(1, 3, 32, 32) print(dummy.device) dummy = dummy.to('cuda') print(dummy.device) dummy = dummy.to('cpu') print(dummy.device)will get:
cpu cuda:0 cpuModel device
class Model(nn.Module): def __init__(self): super().__init__() ... def forward(self, x): ... return x model = Model() model.to('cuda')Be on the same device
All tensors and objects (datasets, models) should be on the same device.
dummy = torch.rand(1, 3, 32, 32).to('cuda') class Model(nn.Module): def __init__(self): super().__init__() self.conv1 = nn.Conv2d(3, 16, kernel_size=3, stride=1, padding=1) self.conv2 = nn.Conv2d(16, 32, kernel_size=3, stride=1, padding=1) self.fc1 = nn.Linear(32 * 32 * 32, 128) self.fc2 = nn.Linear(128, 10) def forward(self, x): x = F.relu(self.conv1(x)) x = F.relu(self.conv2(x)) x = x.view(x.size(0), -1) x = F.relu(self.fc1(x)) x = self.fc2(x) return x model = Model().to('cuda') print(model(dummy).shape)will get:
torch.Size([1, 10])
§1.1.3 Type
numpy.ndarray->torch.Tensor:float64 -> float32
dummy = np.random.rand(1, 3, 32, 32) print(dummy.dtype) dummy = torch.from_numpy(dummy) print(dummy.dtype) print(dummy.device) dummy = dummy.to(torch.float32) print(dummy.dtype)will get:
float64 torch.float64 cpu torch.float32torch.Tensor->numpy.ndarray:cuda->cpu, float32 -> float64dummy = torch.rand(1, 3, 32, 32).to('cuda') print(dummy.dtype) print(dummy.device) dummy = dummy.to('cpu') dummy = dummy.numpy() print(dummy.dtype) dummy = dummy.astype('float64') print(dummy.dtype)will get:
torch.float32 cuda:0 float32 float64
§1.2 torch.nn
nn.Conv2dnn.Conv2d. Convolution is a kind of weighted mean.x = torch.randn(1, 3, 28, 28) print(x.shape) conv2d = nn.Conv2d(in_channels=3, out_channels=12, kernel_size=3) x = conv2d(x) print(x.shape)will get:
torch.Size([1, 3, 28, 28]) torch.Size([1, 12, 26, 26])nn.MaxPool2dx = torch.randn(1, 3, 28, 28) print(x.shape) pool = nn.MaxPool2d(kernel_size=2) x = pool(x) print(x.shape)will get:
torch.Size([1, 3, 28, 28]) torch.Size([1, 3, 14, 14])nn.BatchNorm2dnn.BatchNorm2d, See Fig.2 of [1803.08494] Group Normalization.batchnorm = nn.BatchNorm2d(3) x = torch.randn(1, 3, 3, 3) print(x) x = batchnorm(x) print(x)nn.Linearnn.Linear. For fully connected layer.linear = nn.Linear(3, 12) x = torch.randn(128, 3) x = linear(x) print(x.shape)will get:
torch.Size([128, 12])nn.Dropoutnn.Dropout. For fully connected layer. Using the samples in the Bernoulli distribution, some elements of the input tensor are randomly zeroed with probability $p$. To use it:dropout = nn.Dropout(p=0.5, inplace=False) x = dropout(x)xcan be a tensor in any shape.nn.ReLUorF.relunn.ReLU,F.relu. Activation function, $\text{ReLU}(x)=\max{(0,x)}$, to use it:x = nn.ReLU(x)or:
x = F.relu(x)xcan be a tensor in any shape.nn.RNNinput_size = 10 hidden_size = 20 num_layers = 2 seq_length = 5 batch_size = 3 rnn = nn.RNN(input_size, hidden_size, num_layers) input_data = torch.randn(seq_length, batch_size, input_size) output, hidden_state = rnn(input_data) print(output.shape)will get:
torch.Size([5, 3, 20])nn.Modulenn.Module. Construct a block of layers. It could be the entire model or just a block of the entire model or loss function, etc.class MyBlock(nn.Module): def __init__(self): super().__init__() # define every layer self.conv1 = nn.Conv2d(1, 20, 5) self.conv2 = nn.Conv2d(20, 20, 5) def forward(self, x): # define forward propagation x = F.relu(self.conv1(x)) x = F.relu(self.conv2(x)) return xnn.Sequentialnn.Sequential. Compared withnn.Module,nn.Sequentialcan add the layers more easily and don’t have to define forward propagation. This is more useful when building a simple neural networkmodel = nn.Sequential( nn.Conv2d(1, 20, 5), nn.ReLU(), nn.Conv2d(20, 64, 5), ) x = torch.randn(1, 1, 30, 30) y = model(x) print(y.shape)will get:
torch.Size([1, 64, 22, 22])
§2 CNN
MNIST is here for the purpose of introducing the pipeline of Machine Learning; AlexNet showed the power of cuda and deep neural network; ResNet is the most popular CNN to this day and residual connections are also used in Transformers.
| CNN Explainer | Handwritten Digit Recognizer CNN |
§2.1 MNIST
| mnist (torch) | What is torch.nn really? | MNIST Benchmark | Deep Neural Nets: 33 years ago and 33 years from now |

In mnist (torch):
class Net():
def __init__():
def forward():
def train():
def test():
def main():
if __name__ == '__main__':
main()
Cross Entropy Loss
F.log_softmax,F.nll_loss,F.cross_entropypred = torch.randn(16, 10)# [batch_size, num_classes] target = torch.randint(10, (16,))# [batch_size,] print(F.nll_loss(F.log_softmax(pred, dim=1), target)) print(F.cross_entropy(pred, target))will get:
tensor(2.6026) tensor(2.6026)# same resultclass Netclass Net(nn.Module): def __init__(self): ... def forward(self, x): ... output = F.log_softmax(x, dim=1) return outputsummary(Net(), input_size=(16, 1, 28, 28))# [batch_size, C, H, W]will get:
========================================================================================== Layer (type:depth-idx) Output Shape Param # ========================================================================================== Net [16, 10] -- ├─Conv2d: 1-1 [16, 32, 26, 26] 320 ├─Conv2d: 1-2 [16, 64, 24, 24] 18,496 ├─Dropout: 1-3 [16, 64, 12, 12] -- ├─Linear: 1-4 [16, 128] 1,179,776 ├─Dropout: 1-5 [16, 128] -- ├─Linear: 1-6 [16, 10] 1,290 ========================================================================================== Total params: 1,199,882 Trainable params: 1,199,882 Non-trainable params: 0 Total mult-adds (M): 192.82 ========================================================================================== Input size (MB): 0.05 Forward/backward pass size (MB): 7.51 Params size (MB): 4.80 Estimated Total Size (MB): 12.35 ==========================================================================================def traindef train(args, model, device, train_loader, optimizer, epoch): # set the model to training mode: activate dropout and batch normalization. model.train() # go through each batch. for batch_idx, (data, target) in enumerate(train_loader): # put data and target to device. data, target = data.to(device), target.to(device) # the optimizer's gradient is reset to 0. optimizer.zero_grad() # forward pass. output = model(data) # calculate loss. loss = F.nll_loss(output, target) # calculate the gradients. loss.backward() # backward propagation. optimizer.step() # print loss if batch_idx % args.log_interval == 0: print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format( epoch, batch_idx * len(data), len(train_loader.dataset), 100. * batch_idx / len(train_loader), loss.item())) # if `dry_run`, only run 1 epoch. if args.dry_run: breakdef testdef test(model, device, test_loader): # set the model to evaluation mode. model.eval() test_loss = 0 correct = 0 # gradient calculations are disabled. with torch.no_grad(): for data, target in test_loader: # put data and target to device. data, target = data.to(device), target.to(device) # forward pass. output = model(data) # calculate loss, sum up batch loss. test_loss += F.nll_loss(output, target, reduction='sum').item() # get the index of the max log-probability. pred = output.argmax(dim=1, keepdim=True) # compare predicted labels with target labels. correct += pred.eq(target.view_as(pred)).sum().item() # average loss per sample. test_loss /= len(test_loader.dataset) # print print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format( test_loss, correct, len(test_loader.dataset), 100. * correct / len(test_loader.dataset)))def maindef main(): # Training settings parser = argparse.ArgumentParser(description='PyTorch MNIST Example') parser.add_argument('--batch-size', type=int, default=64, metavar='N', help='input batch size for training (default: 64)') parser.add_argument('--test-batch-size', type=int, default=1000, metavar='N', help='input batch size for testing (default: 1000)') parser.add_argument('--epochs', type=int, default=14, metavar='N', help='number of epochs to train (default: 14)') parser.add_argument('--lr', type=float, default=1.0, metavar='LR', help='learning rate (default: 1.0)') parser.add_argument('--gamma', type=float, default=0.7, metavar='M', help='Learning rate step gamma (default: 0.7)') parser.add_argument('--no-cuda', action='store_true', default=False, help='disables CUDA training') parser.add_argument('--no-mps', action='store_true', default=False, help='disables macOS GPU training') parser.add_argument('--dry-run', action='store_true', default=False, help='quickly check a single pass') parser.add_argument('--seed', type=int, default=1, metavar='S', help='random seed (default: 1)') parser.add_argument('--log-interval', type=int, default=10, metavar='N', help='how many batches to wait before logging training status') parser.add_argument('--save-model', action='store_true', default=False, help='For Saving the current Model') args = parser.parse_args() use_cuda = not args.no_cuda and torch.cuda.is_available() use_mps = not args.no_mps and torch.backends.mps.is_available() torch.manual_seed(args.seed) if use_cuda: device = torch.device("cuda") elif use_mps: device = torch.device("mps") else: device = torch.device("cpu") train_kwargs = {'batch_size': args.batch_size} test_kwargs = {'batch_size': args.test_batch_size} if use_cuda: cuda_kwargs = {'num_workers': 1, 'pin_memory': True, 'shuffle': True} train_kwargs.update(cuda_kwargs) test_kwargs.update(cuda_kwargs) # https://pytorch.org/vision/stable/transforms.html transform=transforms.Compose([ transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,)) ]) # load training dataset and testing dataset dataset1 = datasets.MNIST('../data', train=True, download=True, transform=transform) dataset2 = datasets.MNIST('../data', train=False, transform=transform) train_loader = torch.utils.data.DataLoader(dataset1,**train_kwargs) test_loader = torch.utils.data.DataLoader(dataset2, **test_kwargs) # put model to device model = Net().to(device) # set optimizer and scheduler optimizer = optim.Adadelta(model.parameters(), lr=args.lr) scheduler = StepLR(optimizer, step_size=1, gamma=args.gamma) # train and test for epoch in range(1, args.epochs + 1): train(args, model, device, train_loader, optimizer, epoch) test(model, device, test_loader) scheduler.step() # save model if args.save_model: torch.save(model.state_dict(), "mnist_cnn.pt")
Later we will use fastai instead of writing def train, def test, def main from scratch.
python main.py
will get (full log see 02_mnist.log):
Downloading http://yann.lecun.com/exdb/mnist/train-images-idx3-ubyte.gz
Downloading http://yann.lecun.com/exdb/mnist/train-images-idx3-ubyte.gz to ../data/MNIST/raw/train-images-idx3-ubyte.gz
100% 9912422/9912422 [00:00<00:00, 96238958.45it/s]
Extracting ../data/MNIST/raw/train-images-idx3-ubyte.gz to ../data/MNIST/raw
Downloading http://yann.lecun.com/exdb/mnist/train-labels-idx1-ubyte.gz
Downloading http://yann.lecun.com/exdb/mnist/train-labels-idx1-ubyte.gz to ../data/MNIST/raw/train-labels-idx1-ubyte.gz
100% 28881/28881 [00:00<00:00, 151799115.07it/s]
Extracting ../data/MNIST/raw/train-labels-idx1-ubyte.gz to ../data/MNIST/raw
Downloading http://yann.lecun.com/exdb/mnist/t10k-images-idx3-ubyte.gz
Downloading http://yann.lecun.com/exdb/mnist/t10k-images-idx3-ubyte.gz to ../data/MNIST/raw/t10k-images-idx3-ubyte.gz
100% 1648877/1648877 [00:00<00:00, 27617389.31it/s]
Extracting ../data/MNIST/raw/t10k-images-idx3-ubyte.gz to ../data/MNIST/raw
Downloading http://yann.lecun.com/exdb/mnist/t10k-labels-idx1-ubyte.gz
Downloading http://yann.lecun.com/exdb/mnist/t10k-labels-idx1-ubyte.gz to ../data/MNIST/raw/t10k-labels-idx1-ubyte.gz
100% 4542/4542 [00:00<00:00, 20180644.88it/s]
Extracting ../data/MNIST/raw/t10k-labels-idx1-ubyte.gz to ../data/MNIST/raw
Train Epoch: 1 [0/60000 (0%)] Loss: 2.282550
Train Epoch: 1 [640/60000 (1%)] Loss: 1.384441
...
Train Epoch: 1 [58880/60000 (98%)] Loss: 0.064402
Train Epoch: 1 [59520/60000 (99%)] Loss: 0.033435
Test set: Average loss: 0.0468, Accuracy: 9842/10000 (98%)
Train Epoch: 2 [0/60000 (0%)] Loss: 0.098867
Train Epoch: 2 [640/60000 (1%)] Loss: 0.016046
...
Train Epoch: 2 [58880/60000 (98%)] Loss: 0.108346
Train Epoch: 2 [59520/60000 (99%)] Loss: 0.108657
Test set: Average loss: 0.0327, Accuracy: 9894/10000 (99%)
...
Test set: Average loss: 0.0346, Accuracy: 9887/10000 (99%)
...
Test set: Average loss: 0.0314, Accuracy: 9891/10000 (99%)
...
Test set: Average loss: 0.0301, Accuracy: 9903/10000 (99%)
...
Test set: Average loss: 0.0301, Accuracy: 9913/10000 (99%)
...
Test set: Average loss: 0.0293, Accuracy: 9918/10000 (99%)
...
Test set: Average loss: 0.0295, Accuracy: 9919/10000 (99%)
...
Test set: Average loss: 0.0296, Accuracy: 9915/10000 (99%)
...
Test set: Average loss: 0.0277, Accuracy: 9919/10000 (99%)
...
Test set: Average loss: 0.0284, Accuracy: 9922/10000 (99%)
...
Test set: Average loss: 0.0272, Accuracy: 9922/10000 (99%)
...
Test set: Average loss: 0.0278, Accuracy: 9921/10000 (99%)
...
Test set: Average loss: 0.0278, Accuracy: 9922/10000 (99%)
§2.2 AlexNet: Deep Learning Revolution
ImageNet: 14,197,122 images, 21841 synsets indexed.
| paper | torchvision.models.alexnet | AlexNet (pytorch.org) |
| Methods | Do we use it today? |
|---|---|
2 GPUs: written in cuda, split into 2 different pipelines with connection. | ✔️&✖️ |
| Simple activation function ReLU ($\text{ReLU} (x) = \max{(0,x)}$), instead of Tanh ($\text{Tanh} (x) = \tanh{(x)}$) or Sigmoid ($\sigma (x)= (1+e^{-x})^{-1}$). | ✔️ |
| Local response normalization | ✖️ |
| Overlapping pooling | ✖️ |
| The feature map ($C$) keeps increasing (3 $\to$ 48 $\to$ 128 $\to$ 192 $\to$ 128), while the resolution ($H$, $W$) keeps decreasing (224 $\to$ 55 $\to$ 27 $\to$ 13 $\to$ 13 $\to$ 13). | ✔️ |
| Kernel size keeps decreasing (11 $\to$ 5 $\to$ 3 $\to$ 3 $\to$ 3) | ✖️, same kernel size 3, see ResNet below |
| Multiple linear layers. (take most of the parameters, 55M/61M) | ✖️ |
| Data augmentation (Image translations and horizontal reflections, color jitter) | ✔️, actually this is more data |
| Dropout | ✔️ |
summary(AlexNet(), input_size=(16, 3, 224, 224))
will get:
==========================================================================================
Layer (type:depth-idx) Output Shape Param #
==========================================================================================
AlexNet [16, 1000] --
├─Sequential: 1-1 [16, 256, 6, 6] --
│ └─Conv2d: 2-1 [16, 64, 55, 55] 23,296
│ └─ReLU: 2-2 [16, 64, 55, 55] --
│ └─MaxPool2d: 2-3 [16, 64, 27, 27] --
│ └─Conv2d: 2-4 [16, 192, 27, 27] 307,392
│ └─ReLU: 2-5 [16, 192, 27, 27] --
│ └─MaxPool2d: 2-6 [16, 192, 13, 13] --
│ └─Conv2d: 2-7 [16, 384, 13, 13] 663,936
│ └─ReLU: 2-8 [16, 384, 13, 13] --
│ └─Conv2d: 2-9 [16, 256, 13, 13] 884,992
│ └─ReLU: 2-10 [16, 256, 13, 13] --
│ └─Conv2d: 2-11 [16, 256, 13, 13] 590,080
│ └─ReLU: 2-12 [16, 256, 13, 13] --
│ └─MaxPool2d: 2-13 [16, 256, 6, 6] --
├─AdaptiveAvgPool2d: 1-2 [16, 256, 6, 6] --
├─Sequential: 1-3 [16, 1000] --
│ └─Dropout: 2-14 [16, 9216] --
│ └─Linear: 2-15 [16, 4096] 37,752,832
│ └─ReLU: 2-16 [16, 4096] --
│ └─Dropout: 2-17 [16, 4096] --
│ └─Linear: 2-18 [16, 4096] 16,781,312
│ └─ReLU: 2-19 [16, 4096] --
│ └─Linear: 2-20 [16, 1000] 4,097,000
==========================================================================================
Total params: 61,100,840
Trainable params: 61,100,840
Non-trainable params: 0
Total mult-adds (G): 11.43
==========================================================================================
Input size (MB): 9.63
Forward/backward pass size (MB): 63.26
Params size (MB): 244.40
Estimated Total Size (MB): 317.29
==========================================================================================
§2.3 ResNet: Deeper
| paper | torchvision.models.resnet | ResNet (pytorch.org) |
Problem: With deeper layers, the loss goes upwards (see Fig.1 of the paper), but even if all the added layers are identity functions, the loss would be the same.
| Methods | Do we use it today? |
|---|---|
| Residual connections to learn the differences and go deeper (50, 101, 152, 1202 layers, with 0.85M parameters to 19.4M parameters) | ✔️ |
| The feature map ($C$) keeps increasing (64 $\to$ 128 $\to$ 256 $\to$ 512), while the number of the resolution ($H$, $W$) keeps decreasing (224 $\to$ 112 $\to$ 56 $\to$ 28 $\to$ 14 $\to$ 7 $\to$ 1). | ✔️ |
| Stride 2 convolution kernel, instead of pooling | ✔️ |
| Bottleneck building block: $1 \times 1$ convolution kernel | ✔️&✖️ |
| Adopt batch normalization (BN) right after each convolution and before activation | ✔️&✖️, ongoing debate |
Basically residual is:

Sorry, not that “residual”. 🤣
class Res(nn.Module):
def __init__(self):
super.__init__()
...
def forward(self, x):
residual = x
x = ...(x)
x += residual
residual = x
x = ...(x)
x += residual
return x
By using residual connections, the model will learn linearity first and non-linearity after. We will see residual connections in Transformers.
torchvision.models.resnetdef conv3x3(): def conv1x1(): class BasicBlock(): def __init__(): def forward(): class Bottleneck(): def __init__(): def forward(): class ResNet(): def __init__(): def _make_layer(): def _forward_impl(): def forward(): class ResNet18_Weights(): ... def resnet18(): ...To use it:
from torchvision.models.resnet import resnet18 model = resnet18() summary(model, input_size=(16, 3, 224, 224))or
model = torch.hub.load('pytorch/vision:v0.10.0', 'resnet18', pretrained=True) summary(model, input_size=(16, 3, 224, 224))will get:
Downloading: "https://github.com/pytorch/vision/zipball/v0.10.0" to /root/.cache/torch/hub/v0.10.0.zip /usr/local/lib/python3.10/dist-packages/torchvision/models/_utils.py:208: UserWarning: The parameter 'pretrained' is deprecated since 0.13 and may be removed in the future, please use 'weights' instead. warnings.warn( /usr/local/lib/python3.10/dist-packages/torchvision/models/_utils.py:223: UserWarning: Arguments other than a weight enum or `None` for 'weights' are deprecated since 0.13 and may be removed in the future. The current behavior is equivalent to passing `weights=ResNet18_Weights.IMAGENET1K_V1`. You can also use `weights=ResNet18_Weights.DEFAULT` to get the most up-to-date weights. warnings.warn(msg) Downloading: "https://download.pytorch.org/models/resnet18-f37072fd.pth" to /root/.cache/torch/hub/checkpoints/resnet18-f37072fd.pth 100%|██████████| 44.7M/44.7M [00:00<00:00, 114MB/s] ========================================================================================== Layer (type:depth-idx) Output Shape Param # ========================================================================================== ResNet [16, 1000] -- ├─Conv2d: 1-1 [16, 64, 112, 112] 9,408 ├─BatchNorm2d: 1-2 [16, 64, 112, 112] 128 ├─ReLU: 1-3 [16, 64, 112, 112] -- ├─MaxPool2d: 1-4 [16, 64, 56, 56] -- ├─Sequential: 1-5 [16, 64, 56, 56] -- │ └─BasicBlock: 2-1 [16, 64, 56, 56] -- │ │ └─Conv2d: 3-1 [16, 64, 56, 56] 36,864 │ │ └─BatchNorm2d: 3-2 [16, 64, 56, 56] 128 │ │ └─ReLU: 3-3 [16, 64, 56, 56] -- │ │ └─Conv2d: 3-4 [16, 64, 56, 56] 36,864 │ │ └─BatchNorm2d: 3-5 [16, 64, 56, 56] 128 │ │ └─ReLU: 3-6 [16, 64, 56, 56] -- │ └─BasicBlock: 2-2 [16, 64, 56, 56] -- │ │ └─Conv2d: 3-7 [16, 64, 56, 56] 36,864 │ │ └─BatchNorm2d: 3-8 [16, 64, 56, 56] 128 │ │ └─ReLU: 3-9 [16, 64, 56, 56] -- │ │ └─Conv2d: 3-10 [16, 64, 56, 56] 36,864 │ │ └─BatchNorm2d: 3-11 [16, 64, 56, 56] 128 │ │ └─ReLU: 3-12 [16, 64, 56, 56] -- ├─Sequential: 1-6 [16, 128, 28, 28] -- │ └─BasicBlock: 2-3 [16, 128, 28, 28] -- │ │ └─Conv2d: 3-13 [16, 128, 28, 28] 73,728 │ │ └─BatchNorm2d: 3-14 [16, 128, 28, 28] 256 │ │ └─ReLU: 3-15 [16, 128, 28, 28] -- │ │ └─Conv2d: 3-16 [16, 128, 28, 28] 147,456 │ │ └─BatchNorm2d: 3-17 [16, 128, 28, 28] 256 │ │ └─Sequential: 3-18 [16, 128, 28, 28] 8,448 │ │ └─ReLU: 3-19 [16, 128, 28, 28] -- │ └─BasicBlock: 2-4 [16, 128, 28, 28] -- │ │ └─Conv2d: 3-20 [16, 128, 28, 28] 147,456 │ │ └─BatchNorm2d: 3-21 [16, 128, 28, 28] 256 │ │ └─ReLU: 3-22 [16, 128, 28, 28] -- │ │ └─Conv2d: 3-23 [16, 128, 28, 28] 147,456 │ │ └─BatchNorm2d: 3-24 [16, 128, 28, 28] 256 │ │ └─ReLU: 3-25 [16, 128, 28, 28] -- ├─Sequential: 1-7 [16, 256, 14, 14] -- │ └─BasicBlock: 2-5 [16, 256, 14, 14] -- │ │ └─Conv2d: 3-26 [16, 256, 14, 14] 294,912 │ │ └─BatchNorm2d: 3-27 [16, 256, 14, 14] 512 │ │ └─ReLU: 3-28 [16, 256, 14, 14] -- │ │ └─Conv2d: 3-29 [16, 256, 14, 14] 589,824 │ │ └─BatchNorm2d: 3-30 [16, 256, 14, 14] 512 │ │ └─Sequential: 3-31 [16, 256, 14, 14] 33,280 │ │ └─ReLU: 3-32 [16, 256, 14, 14] -- │ └─BasicBlock: 2-6 [16, 256, 14, 14] -- │ │ └─Conv2d: 3-33 [16, 256, 14, 14] 589,824 │ │ └─BatchNorm2d: 3-34 [16, 256, 14, 14] 512 │ │ └─ReLU: 3-35 [16, 256, 14, 14] -- │ │ └─Conv2d: 3-36 [16, 256, 14, 14] 589,824 │ │ └─BatchNorm2d: 3-37 [16, 256, 14, 14] 512 │ │ └─ReLU: 3-38 [16, 256, 14, 14] -- ├─Sequential: 1-8 [16, 512, 7, 7] -- │ └─BasicBlock: 2-7 [16, 512, 7, 7] -- │ │ └─Conv2d: 3-39 [16, 512, 7, 7] 1,179,648 │ │ └─BatchNorm2d: 3-40 [16, 512, 7, 7] 1,024 │ │ └─ReLU: 3-41 [16, 512, 7, 7] -- │ │ └─Conv2d: 3-42 [16, 512, 7, 7] 2,359,296 │ │ └─BatchNorm2d: 3-43 [16, 512, 7, 7] 1,024 │ │ └─Sequential: 3-44 [16, 512, 7, 7] 132,096 │ │ └─ReLU: 3-45 [16, 512, 7, 7] -- │ └─BasicBlock: 2-8 [16, 512, 7, 7] -- │ │ └─Conv2d: 3-46 [16, 512, 7, 7] 2,359,296 │ │ └─BatchNorm2d: 3-47 [16, 512, 7, 7] 1,024 │ │ └─ReLU: 3-48 [16, 512, 7, 7] -- │ │ └─Conv2d: 3-49 [16, 512, 7, 7] 2,359,296 │ │ └─BatchNorm2d: 3-50 [16, 512, 7, 7] 1,024 │ │ └─ReLU: 3-51 [16, 512, 7, 7] -- ├─AdaptiveAvgPool2d: 1-9 [16, 512, 1, 1] -- ├─Linear: 1-10 [16, 1000] 513,000 ========================================================================================== Total params: 11,689,512 Trainable params: 11,689,512 Non-trainable params: 0 Total mult-adds (G): 29.03 ========================================================================================== Input size (MB): 9.63 Forward/backward pass size (MB): 635.96 Params size (MB): 46.76 Estimated Total Size (MB): 692.35 ==========================================================================================Homemade
ResNet18class ResidualBlock(nn.Module): def __init__(self, in_channels, out_channels, stride=1): super().__init__() self.conv1 = nn.Conv2d(in_channels, out_channels, kernel_size=3, stride=stride, padding=1, bias=False) self.bn1 = nn.BatchNorm2d(out_channels) self.relu = nn.ReLU() self.conv2 = nn.Conv2d(out_channels, out_channels, kernel_size=3, stride=1, padding=1, bias=False) self.bn2 = nn.BatchNorm2d(out_channels) if stride != 1 or in_channels != out_channels: self.residual = nn.Sequential( nn.Conv2d(in_channels, out_channels, stride=stride, kernel_size=1, bias=False), nn.BatchNorm2d(out_channels) ) else: self.residual = nn.Identity() def forward(self, x): residual = x x = self.conv1(x) x = self.bn1(x) x = self.relu(x) x = self.conv2(x) x = self.bn2(x) x += self.residual(residual) x = self.relu(x) return xclass ResNet18(nn.Module): def __init__(self, num_classes=1000): super().__init__() self.conv1 = nn.Conv2d(3, 64, kernel_size=7, stride=2, padding=3, bias=False) self.bn1 = nn.BatchNorm2d(64) self.relu = nn.ReLU() self.maxpool = nn.MaxPool2d(kernel_size=3, stride=2, padding=1) self.layer1 = self._make_layer(64, 64, num_layers=2, stride=1) self.layer2 = self._make_layer(64, 128, num_layers=2, stride=2) self.layer3 = self._make_layer(128, 256, num_layers=2, stride=2) self.layer4 = self._make_layer(256, 512, num_layers=2, stride=2) self.avgpool = nn.AdaptiveAvgPool2d((1,1)) self.fc = nn.Linear(512, num_classes)# fully connected def _make_layer(self, in_channels, out_channels, num_layers, stride=1): layers = [] layers.append(ResidualBlock(in_channels, out_channels, stride)) for _ in range(1, num_layers): layers.append(ResidualBlock(out_channels, out_channels)) return nn.Sequential(*layers) def forward(self, x): x = self.conv1(x) x = self.bn1(x) x = self.relu(x) x = self.maxpool(x) x = self.layer1(x) x = self.layer2(x) x = self.layer3(x) x = self.layer4(x) x = self.avgpool(x) x = x.view(x.size(0), -1) x = self.fc(x) return xsummary(ResNet18(), input_size = (16, 3, 224, 224))will get:
========================================================================================== Layer (type:depth-idx) Output Shape Param # ========================================================================================== ResNet18 [16, 1000] -- ├─Conv2d: 1-1 [16, 64, 112, 112] 9,408 ├─BatchNorm2d: 1-2 [16, 64, 112, 112] 128 ├─ReLU: 1-3 [16, 64, 112, 112] -- ├─MaxPool2d: 1-4 [16, 64, 56, 56] -- ├─Sequential: 1-5 [16, 64, 56, 56] -- │ └─ResidualBlock: 2-1 [16, 64, 56, 56] -- │ │ └─Conv2d: 3-1 [16, 64, 56, 56] 36,864 │ │ └─BatchNorm2d: 3-2 [16, 64, 56, 56] 128 │ │ └─ReLU: 3-3 [16, 64, 56, 56] -- │ │ └─Conv2d: 3-4 [16, 64, 56, 56] 36,864 │ │ └─BatchNorm2d: 3-5 [16, 64, 56, 56] 128 │ │ └─Identity: 3-6 [16, 64, 56, 56] -- │ │ └─ReLU: 3-7 [16, 64, 56, 56] -- │ └─ResidualBlock: 2-2 [16, 64, 56, 56] -- │ │ └─Conv2d: 3-8 [16, 64, 56, 56] 36,864 │ │ └─BatchNorm2d: 3-9 [16, 64, 56, 56] 128 │ │ └─ReLU: 3-10 [16, 64, 56, 56] -- │ │ └─Conv2d: 3-11 [16, 64, 56, 56] 36,864 │ │ └─BatchNorm2d: 3-12 [16, 64, 56, 56] 128 │ │ └─Identity: 3-13 [16, 64, 56, 56] -- │ │ └─ReLU: 3-14 [16, 64, 56, 56] -- ├─Sequential: 1-6 [16, 128, 28, 28] -- │ └─ResidualBlock: 2-3 [16, 128, 28, 28] -- │ │ └─Conv2d: 3-15 [16, 128, 28, 28] 73,728 │ │ └─BatchNorm2d: 3-16 [16, 128, 28, 28] 256 │ │ └─ReLU: 3-17 [16, 128, 28, 28] -- │ │ └─Conv2d: 3-18 [16, 128, 28, 28] 147,456 │ │ └─BatchNorm2d: 3-19 [16, 128, 28, 28] 256 │ │ └─Sequential: 3-20 [16, 128, 28, 28] 8,448 │ │ └─ReLU: 3-21 [16, 128, 28, 28] -- │ └─ResidualBlock: 2-4 [16, 128, 28, 28] -- │ │ └─Conv2d: 3-22 [16, 128, 28, 28] 147,456 │ │ └─BatchNorm2d: 3-23 [16, 128, 28, 28] 256 │ │ └─ReLU: 3-24 [16, 128, 28, 28] -- │ │ └─Conv2d: 3-25 [16, 128, 28, 28] 147,456 │ │ └─BatchNorm2d: 3-26 [16, 128, 28, 28] 256 │ │ └─Identity: 3-27 [16, 128, 28, 28] -- │ │ └─ReLU: 3-28 [16, 128, 28, 28] -- ├─Sequential: 1-7 [16, 256, 14, 14] -- │ └─ResidualBlock: 2-5 [16, 256, 14, 14] -- │ │ └─Conv2d: 3-29 [16, 256, 14, 14] 294,912 │ │ └─BatchNorm2d: 3-30 [16, 256, 14, 14] 512 │ │ └─ReLU: 3-31 [16, 256, 14, 14] -- │ │ └─Conv2d: 3-32 [16, 256, 14, 14] 589,824 │ │ └─BatchNorm2d: 3-33 [16, 256, 14, 14] 512 │ │ └─Sequential: 3-34 [16, 256, 14, 14] 33,280 │ │ └─ReLU: 3-35 [16, 256, 14, 14] -- │ └─ResidualBlock: 2-6 [16, 256, 14, 14] -- │ │ └─Conv2d: 3-36 [16, 256, 14, 14] 589,824 │ │ └─BatchNorm2d: 3-37 [16, 256, 14, 14] 512 │ │ └─ReLU: 3-38 [16, 256, 14, 14] -- │ │ └─Conv2d: 3-39 [16, 256, 14, 14] 589,824 │ │ └─BatchNorm2d: 3-40 [16, 256, 14, 14] 512 │ │ └─Identity: 3-41 [16, 256, 14, 14] -- │ │ └─ReLU: 3-42 [16, 256, 14, 14] -- ├─Sequential: 1-8 [16, 512, 7, 7] -- │ └─ResidualBlock: 2-7 [16, 512, 7, 7] -- │ │ └─Conv2d: 3-43 [16, 512, 7, 7] 1,179,648 │ │ └─BatchNorm2d: 3-44 [16, 512, 7, 7] 1,024 │ │ └─ReLU: 3-45 [16, 512, 7, 7] -- │ │ └─Conv2d: 3-46 [16, 512, 7, 7] 2,359,296 │ │ └─BatchNorm2d: 3-47 [16, 512, 7, 7] 1,024 │ │ └─Sequential: 3-48 [16, 512, 7, 7] 132,096 │ │ └─ReLU: 3-49 [16, 512, 7, 7] -- │ └─ResidualBlock: 2-8 [16, 512, 7, 7] -- │ │ └─Conv2d: 3-50 [16, 512, 7, 7] 2,359,296 │ │ └─BatchNorm2d: 3-51 [16, 512, 7, 7] 1,024 │ │ └─ReLU: 3-52 [16, 512, 7, 7] -- │ │ └─Conv2d: 3-53 [16, 512, 7, 7] 2,359,296 │ │ └─BatchNorm2d: 3-54 [16, 512, 7, 7] 1,024 │ │ └─Identity: 3-55 [16, 512, 7, 7] -- │ │ └─ReLU: 3-56 [16, 512, 7, 7] -- ├─AdaptiveAvgPool2d: 1-9 [16, 512, 1, 1] -- ├─Linear: 1-10 [16, 1000] 513,000 ========================================================================================== Total params: 11,689,512 Trainable params: 11,689,512 Non-trainable params: 0 Total mult-adds (G): 29.03 ========================================================================================== Input size (MB): 9.63 Forward/backward pass size (MB): 635.96 Params size (MB): 46.76 Estimated Total Size (MB): 692.35 ==========================================================================================
§3 Transformer
Transformer is a general function fitter.
§3.1 Embedding
Embedding is ordered higher-dimensional representation vectors.
§3.1.1 nn.Embedding
Words in hidden_dim vector space: $\vec{R} + \vec{L} = \vec{J}$, $\vec{king} - \vec{man} = \vec{queen} - \vec{woman}$.
nn.EmbeddingNUM_INDEX = 3 EMBEDDING_DIM = 4 embedding = nn.Embedding(NUM_INDEX, EMBEDDING_DIM) print(embedding.weight.detach()) index = torch.LongTensor([2, 0]) print(embedding(index))will get:
tensor([[ 0.0378, 1.0396, -0.9673, 0.9697], [-0.7824, 1.8141, 0.5336, -1.6396], [ 0.1903, 0.6592, 1.4589, -0.6018]]) tensor([[ 0.1903, 0.6592, 1.4589, -0.6018], [ 0.0378, 1.0396, -0.9673, 0.9697]], grad_fn=<EmbeddingBackward0>)F.one_hotthen linearone_hot = F.one_hot(index, num_classes=NUM_INDEX) print(one_hot) linear = nn.Linear(NUM_INDEX, EMBEDDING_DIM, bias=False) linear.weight = nn.Parameter(embedding.weight.T.detach()) print(linear(one_hot.float()))will get:
tensor([[0, 0, 1], [1, 0, 0]]) tensor([[ 0.1903, 0.6592, 1.4589, -0.6018], [ 0.0378, 1.0396, -0.9673, 0.9697]], grad_fn=<MmBackward0>)# same result
§3.1.2 Sinusoidal Positional Embedding
class Embeddingclass Embedding(nn.Module): def __init__(self, hidden_dim=768, vocab_size=50257): super().__init__() self.embedding = nn.Embedding(vocab_size, hidden_dim) self.hidden_dim = hidden_dim def forward(self, x): return self.embedding(x) * math.sqrt(self.hidden_dim)class PositionalEncodingThe positional encoding $$\begin{aligned} PE_{(pos, 2i)} &= \sin(\frac{pos}{ 10000^{2i/{d_{model}}}}) \\ PE_{(pos, 2i + 1)} &= \cos(\frac{pos}{10000^{2i/{d_{model}}}}) \end{aligned}$$, where $pos$ is each element in the sequence up to
vocab_size, and $d_{model}$ ishidden_dim.class PositionalEncoding(nn.Module): def __init__(self, hidden_dim=768, vocab_size=50257, dropout=0.0): super().__init__() self.dropout = nn.Dropout(dropout) pe = torch.zeros(vocab_size, hidden_dim) position = torch.arange(0, vocab_size).unsqueeze(1) div_term = torch.exp(torch.arange(0, hidden_dim, 2) * -(math.log(10000.0) / hidden_dim)) pe[:, 0::2] = torch.sin(position * div_term) pe[:, 1::2] = torch.cos(position * div_term) pe = pe.unsqueeze(0) self.pe = pe def forward(self, x): seq_length = x.shape[1] x = x + self.pe[:, :seq_length].requires_grad_(False) return self.dropout(x)testing
dummy = torch.randint(50257, (1, 196))# [batch_size, seq_length], words as int numbers embeddings = Embedding() dummy = embeddings(dummy) print(dummy.shape)# [batch_size, seq_length, hidden_dim] positional_encoding = PositionalEncoding() dummy = positional_encoding(dummy) print(dummy.shape)# [batch_size, seq_length, hidden_dim]will get:
torch.Size([1, 196, 768]) torch.Size([1, 196, 768])
We will often see another way to write it:
class SinusoidalPosEmbclass SinusoidalPosEmb(nn.Module): def __init__(self, hidden_dim=768, M=10000): super().__init__() self.hidden_dim = hidden_dim self.M = M def forward(self, x): device = x.device half_dim = self.hidden_dim // 2 emb = math.log(self.M) / half_dim emb = torch.exp(torch.arange(half_dim, device=device) * (-emb)) emb = x[..., None] * emb[None, ...] emb = torch.cat((emb.sin(), emb.cos()), dim=-1) return embtesting
dummy = torch.rand(1, 196)# [batch_size, seq_length], words as float numbers sinusoidal_pos_emb = SinusoidalPosEmb() dummy = sinusoidal_pos_emb(dummy) print(dummy.shape)# [batch_size, seq_length, hidden_dim]will get:
torch.Size([1, 196, 768])
§3.2 Transformer Encoder
§3.2.1 FFN (MLP)
A Neural Probabilistic Language Model
Equation
Feed Forward Network works on each
[seq_length, ]vector individually $$\text{FFN}(x)=(\text{ReLU}(xW_1+b_1))W_2+b_2$$, where $\text{ReLU}(x)=\max{(0,x)}$. Here we replacenn.ReLUwithnn.GELU.class FFNclass FFN(nn.Module): def __init__(self, in_features=768, hidden_features=3072, out_features=768, dropout=0.0): super().__init__() self.linear1 = nn.Linear(in_features, hidden_features) self.act = nn.GELU() self.linear2 = nn.Linear(hidden_features, out_features) self.dropout = nn.Dropout(dropout) def forward(self, x): x = self.linear1(x) x = self.act(x) x = self.dropout(x) x = self.linear2(x) x = self.dropout(x) return xclass FFN(nn.Sequential): def __init__(self, in_features=768, hidden_features=3072, out_features=768, dropout=0.0): super().__init__() nn.Linear(in_features, hidden_features), nn.GELU(), nn.Dropout(dropout), nn.Linear(hidden_features, out_features), nn.Dropout(dropout)testing
dummy = torch.rand(1, 196, 768)# [batch_size, seq_length, hidden_dim] ffn = FFN() dummy = ffn(dummy) print(dummy.shape)will get:
torch.Size([1, 196, 768])
§3.2.2 MultiheadAttention
nn.MultiheadAttention, F.scaled_dot_product_attention, FlexAttention
Equation
Self-Attention: Given an input $x$, we will get query $Q$, key $K$, value $V$ by $$\begin{aligned} Q&=xW^Q \\ K&=xW^K \\ V&=xW^V\end{aligned}$$Then $$\text{Attention}(Q, K, V) = \frac{1}{\sqrt{d_{k}}}\text{Softmax}(QK^\mathsf{T})V$$, where for a vector $\vec{z_i}$, $\text{Softmax}(\vec{z_i}) = \frac{e^{\vec{z_i}}}{\sum_{i=0}^N e^{\vec{z_i}}}$, and $$\text{MultiheadAttention} (Q, K, V) = \text{Concat}(\text{head}_1, \cdots, \text{head}_h) W^O$$, where $\text{head}_i = \text{Attention} (xW^Q_i, xW^K_i, xW^V_i)$, and $h$ is
num_headsin the code.The advantage of Softmax:
- Matthew effect
- Non-linearity
- Normalization
Note that in the figure below, only
q_size = k_sizeis necessary. But in the code,q_size = k_size = v_size = hidden_dim.class MultiheadAttentionclass MultiheadAttention(nn.Module): def __init__(self, hidden_dim=768, num_heads=12, dropout=0.0): super().__init__() self.num_heads = num_heads self.scale = (hidden_dim // num_heads) ** -0.5 self.w_qkv = nn.Linear(hidden_dim, hidden_dim * 3) self.w_o = nn.Linear(hidden_dim, hidden_dim) self.dropout = nn.Dropout(dropout) def forward(self, x, is_causal=False): batch_size, seq_length, hidden_dim = x.shape qkv = self.w_qkv(x)# [batch_size, seq_length, hidden_dim * 3] qkv = qkv.view(batch_size, seq_length, 3, self.num_heads, -1)# [batch_size, seq_length, 3, num_heads, hidden_dim // num_heads] qkv = qkv.permute(2, 0, 3, 1, 4)# [3, batch_size, num_heads, seq_length, hidden_dim // num_heads] q, k, v = qkv# q, k, v shape: [batch_size, num_heads, seq_length, hidden_dim // num_heads] # attn shape: [batch_size, num_heads, seq_length, seq_length] attn = self.scale * q @ (k.transpose(-2, -1))# `torch.matmul` if is_causal:# masked/causal attention attn = attn.masked_fill_(# `torch.Tensor.masked_fill_`, add mask by broadcasting torch.triu(torch.ones((seq_length, seq_length), dtype=torch.bool), diagonal=1), float('-inf') ) attn = attn.softmax(dim=-1) attn = self.dropout(attn) x = attn @ v# [batch_size, num_heads, seq_length, hidden_dim // num_heads] x = x.transpose(1, 2)# [batch_size, seq_length, num_heads, hidden_dim // num_heads] x = x.reshape(batch_size, seq_length, hidden_dim)# [batch_size, seq_length, hidden_dim] x = self.w_o(x)# [batch_size, seq_length, hidden_dim] x = self.dropout(x) return xtesting
Add 4 lines of
print():class MultiheadAttention(nn.Module): def __init__(self, hidden_dim=768, num_heads=12, dropout=0.0): super().__init__() self.num_heads = num_heads self.scale = (hidden_dim // num_heads) ** -0.5 self.w_qkv = nn.Linear(hidden_dim, hidden_dim * 3) self.w_o = nn.Linear(hidden_dim, hidden_dim) self.dropout = nn.Dropout(dropout) def forward(self, x, is_causal=False): batch_size, seq_length, hidden_dim = x.shape qkv = self.w_qkv(x)# [batch_size, seq_length, hidden_dim * 3] qkv = qkv.view(batch_size, seq_length, 3, self.num_heads, -1)# [batch_size, seq_length, 3, num_heads, hidden_dim // num_heads] qkv = qkv.permute(2, 0, 3, 1, 4)# [3, batch_size, num_heads, seq_length, hidden_dim // num_heads] q, k, v = qkv# q, k, v shape: [batch_size, num_heads, seq_length, hidden_dim // num_heads] # attn shape: [batch_size, num_heads, seq_length, seq_length] attn = self.scale * q @ (k.transpose(-2, -1))# `torch.matmul` if is_causal:# masked/causal attention attn = attn.masked_fill_(# `torch.Tensor.masked_fill_`, add mask by broadcasting torch.triu(torch.ones((seq_length, seq_length), dtype=torch.bool), diagonal=1), float('-inf') ) print(attn) print(attn.shape) attn = attn.softmax(dim=-1) print(attn) print(attn.shape) attn = self.dropout(attn) x = attn @ v# [batch_size, num_heads, seq_length, hidden_dim // num_heads] x = x.transpose(1, 2)# [batch_size, seq_length, num_heads, hidden_dim // num_heads] x = x.reshape(batch_size, seq_length, hidden_dim)# [batch_size, seq_length, hidden_dim] x = self.w_o(x)# [batch_size, seq_length, hidden_dim] x = self.dropout(x) return xdummy = torch.rand(1, 4, 6)# [batch_size, seq_length, hidden_dim] multihead_attention = MultiheadAttention(hidden_dim=6, num_heads=2) print('No mask:') _ = multihead_attention(dummy) print('Masked:') _ = multihead_attention(dummy, is_causal=True)will get:
No mask: tensor([[[[-0.0302, -0.0241, -0.0071, -0.0822], [ 0.0041, 0.0307, 0.0372, -0.0366], [-0.0460, -0.0571, 0.1467, 0.1020], [-0.0685, -0.0811, 0.1513, 0.0700]], [[ 0.0744, 0.0987, 0.2944, 0.3069], [ 0.0538, 0.0855, 0.2632, 0.2898], [-0.0052, 0.0453, 0.1585, 0.2132], [ 0.0034, 0.0774, 0.2627, 0.3394]]]], grad_fn=<UnsafeViewBackward0>) torch.Size([1, 2, 4, 4])# [batch_size, num_heads, seq_length, seq_length] tensor([[[[0.2513, 0.2529, 0.2572, 0.2386], [0.2487, 0.2554, 0.2571, 0.2388], [0.2293, 0.2268, 0.2780, 0.2659], [0.2282, 0.2254, 0.2843, 0.2621]], [[0.2206, 0.2261, 0.2749, 0.2784], [0.2207, 0.2278, 0.2721, 0.2794], [0.2235, 0.2351, 0.2633, 0.2781], [0.2095, 0.2256, 0.2716, 0.2932]]]], grad_fn=<SoftmaxBackward0>) torch.Size([1, 2, 4, 4]) Masked: tensor([[[[-0.0302, -inf, -inf, -inf], [ 0.0041, 0.0307, -inf, -inf], [-0.0460, -0.0571, 0.1467, -inf], [-0.0685, -0.0811, 0.1513, 0.0700]], [[ 0.0744, -inf, -inf, -inf], [ 0.0538, 0.0855, -inf, -inf], [-0.0052, 0.0453, 0.1585, -inf], [ 0.0034, 0.0774, 0.2627, 0.3394]]]], grad_fn=<MaskedFillBackward0>) torch.Size([1, 2, 4, 4]) tensor([[[[1.0000, 0.0000, 0.0000, 0.0000], [0.4934, 0.5066, 0.0000, 0.0000], [0.3124, 0.3089, 0.3787, 0.0000], [0.2282, 0.2254, 0.2843, 0.2621]], [[1.0000, 0.0000, 0.0000, 0.0000], [0.4921, 0.5079, 0.0000, 0.0000], [0.3096, 0.3257, 0.3647, 0.0000], [0.2095, 0.2256, 0.2716, 0.2932]]]], grad_fn=<SoftmaxBackward0>) torch.Size([1, 2, 4, 4])
Use F.scaled_dot_product_attention:
class MultiheadAttention(nn.Module):
def __init__(self, hidden_dim=768, num_heads=12, dropout=0.0):
super().__init__()
self.num_heads = num_heads
self.dropout = dropout
self.w_qkv = nn.Linear(hidden_dim, hidden_dim * 3)
self.w_o = nn.Linear(hidden_dim, hidden_dim)
def forward(self, x, is_causal=False):
batch_size, seq_length, hidden_dim = x.shape
qkv = self.w_qkv(x)# [batch_size, seq_length, hidden_dim * 3]
qkv = qkv.view(batch_size, seq_length, 3, self.num_heads, -1)# [batch_size, seq_length, 3, num_heads, hidden_dim // num_heads]
qkv = qkv.permute(2, 0, 3, 1, 4)# [3, batch_size, num_heads, seq_length, hidden_dim // num_heads]
q, k, v = qkv# q, k, v shape: [batch_size, num_heads, seq_length, hidden_dim // num_heads]
x = F.scaled_dot_product_attention(q, k, v, dropout_p=self.dropout, is_causal=is_causal)# [batch_size, num_heads, seq_length, hidden_dim // num_heads]
x = x.transpose(1, 2)# [batch_size, seq_length, num_heads, hidden_dim // num_heads]
x = x.view(batch_size, seq_length, hidden_dim)# [batch_size, seq_length, hidden_dim]
x = self.w_o(x)# [batch_size, seq_length, hidden_dim]
return x
dummy = torch.rand(1, 196, 768)# [batch_size, seq_length, hidden_dim]
multihead_attention = MultiheadAttention()
dummy = multihead_attention(dummy)
print(dummy.shape)
will get:
torch.Size([1, 196, 768])
§3.2.3 TransformerEncoderLayer
class TransformerEncoderLayer(nn.Module):
def __init__(self, num_layers=12, num_heads=12, hidden_dim=768, ffn_dim=3072, dropout=0.0):
super().__init__()
self.layer_norm_1 = nn.LayerNorm(hidden_dim)
self.attention = MultiheadAttention(hidden_dim, num_heads, dropout)
self.layer_norm_2 = nn.LayerNorm(hidden_dim)
self.ffn = FFN(hidden_dim, ffn_dim, hidden_dim, dropout)
self.dropout = nn.Dropout(dropout)
self.attn_scale = 1 / math.sqrt(2 * num_layersr)
def forward(self, x):
residual = x
x = self.layer_norm_1(x)
x = self.attn_scale * self.attention(x)
x = self.dropout(x)
x += residual
residual = x
x = self.layer_norm_2(x)
x = self.ffn(x)
x = self.dropout(x)
x += residual
return x
In contrast with the Original Transformer, Layer Norm is put before Attention, see [2002.04745] On Layer Normalization in the Transformer Architecture.
summary(TransformerEncoderLayer(), input_size=(1, 196, 768))
will get:
==========================================================================================
Layer (type:depth-idx) Output Shape Param #
==========================================================================================
TransformerEncoderLayer [1, 196, 768] --
├─LayerNorm: 1-1 [1, 196, 768] 1,536
├─MultiheadAttention: 1-2 [1, 196, 768] --
│ └─Linear: 2-1 [1, 196, 2304] 1,771,776
│ └─Dropout: 2-2 [1, 12, 196, 196] --
│ └─Linear: 2-3 [1, 196, 768] 590,592
│ └─Dropout: 2-4 [1, 196, 768] --
├─Dropout: 1-3 [1, 196, 768] --
├─LayerNorm: 1-4 [1, 196, 768] 1,536
├─FFN: 1-5 [1, 196, 768] --
│ └─Linear: 2-5 [1, 196, 3072] 2,362,368
│ └─GELU: 2-6 [1, 196, 3072] --
│ └─Dropout: 2-7 [1, 196, 3072] --
│ └─Linear: 2-8 [1, 196, 768] 2,360,064
│ └─Dropout: 2-9 [1, 196, 768] --
├─Dropout: 1-6 [1, 196, 768] --
==========================================================================================
Total params: 7,087,872
Trainable params: 7,087,872
Non-trainable params: 0
Total mult-adds (M): 7.09
==========================================================================================
Input size (MB): 0.60
Forward/backward pass size (MB): 13.25
Params size (MB): 28.35
Estimated Total Size (MB): 42.20
==========================================================================================
Most of the parameters is in FNN rather than MultiheadAttention. FFN takes 66.66%, while MultiheadAttention takes 33.33%. This is even more so with MoE, which has several FFNs.
§3.2.4 TransformerEncoder
class TransformerEncoder(nn.Module):
def __init__(self, num_layers=12, num_heads=12, hidden_dim=768, ffn_dim=3072, dropout=0.0):
super().__init__()
self.transformer_encoder_layers = nn.ModuleList([
TransformerEncoderLayer(num_layers, num_heads, hidden_dim, ffn_dim, dropout)
for _ in range(num_layers)
])
def forward(self, x):
for transformer_encoder_layer in self.transformer_encoder_layers:
x = transformer_encoder_layer(x)
return x
§3.3 Encoder-Decoder, Encoder-Only, Decoder-Only
| Encoder-Decoder: seq2seq | Encoder-Decoder: Transformer |
|---|---|
| Understanding Transformer model architectures (practicalai.io) | 11.9. Large-Scale Pretraining with Transformers (d2l.ai) |
| NLP | CV | |
|---|---|---|
| Encoder-Decoder | [1706.03762] Attention is All You Need, T5 | BEiT |
| Encoder-Only | BERT | ViT |
| Decoder-Only | GPT, GPT-2, GPT-3, nanoGPT, modded-nanogpt |
Fig.1 of [2304.13712] Harnessing the Power of LLMs in Practice: A Survey on ChatGPT and Beyond:
| Original Transformer, Encoder | Original Transformer, Decoder | ViT (Encoder-Only) | GPT (Decoder-Only) | |
|---|---|---|---|---|
| Self-Attention or Cross-Attention | Self-Attention | The first Self-Attention, the second Cross-Attention | Self-Attention | Self-Attention |
| Mask/Causal | ✖️ | ✔️ | ✖️ | ✔️ |
§3.4 Attention is All You Need (the Original Transformer)
[1706.03762] Attention Is All You Need
- A pure Transformer structure instead of RNNs.
- Use Softmax to let query $Q$ choose different $K^\mathsf{T}$.
- The encoder provides keys $K$ and value $V$, while the decoder provides query $Q$. (Cross-Attention)
§3.5 Vision Transformer (ViT)
[2010.11929] An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale
- A pure Transformer structure instead of CNNs.
- General function fitter instead of good inductive prior.
- With enough data.
§3.5.1 PatchEmbedding
class PatchEmbeddingclass PatchEmbedding(nn.Module): def __init__(self, in_channels=3, patch_size=16, hidden_dim=768): super().__init__() self.conv2d = nn.Conv2d( in_channels=in_channels, out_channels=hidden_dim, kernel_size=patch_size, stride=patch_size, padding=0 ) self.hidden_dim = hidden_dim def forward(self, x): batch_size = x.shape[0] x = self.conv2d(x) x = x.view(batch_size, -1, self.hidden_dim) return xclass PatchEmbedding_noConvor without convolution:
class PatchEmbedding_noConv(nn.Module): def __init__(self, hidden_dim=768): super().__init__() self.hidden_dim = hidden_dim def forward(self, x): batch_size = x.shape[0] x = x.view(batch_size, -1, self.hidden_dim) return x
§3.5.2 VisionTransformer
Homemade
TransformerEncoderclass VisionTransformer(nn.Module): def __init__( self, image_size=224, in_channels=3, patch_size=16, num_classes=1000, num_layers=12, num_heads=12, hidden_dim=768, ffn_dim=3072, dropout=0.0 ): super().__init__() self.patch_embedding = PatchEmbedding(in_channels, patch_size, hidden_dim) self.pos_embedding = nn.Parameter(torch.empty(1, (image_size // patch_size)**2, hidden_dim).normal_(std=0.02)) self.class_token = nn.Parameter(torch.empty(1, 1, hidden_dim)) self.transformer_encoder = TransformerEncoder(num_layers, num_heads, hidden_dim, ffn_dim, dropout) # self.layer_norm = nn.LayerNorm(hidden_dim) self.proj = nn.Linear(hidden_dim, num_classes) def forward(self, x): x = self.patch_embedding(x) x += self.pos_embedding batch_size = x.shape[0] batch_class_token = self.class_token.expand(batch_size, -1, -1) x = torch.cat([batch_class_token, x], dim=1) x = self.transformer_encoder(x) # x = self.layer_norm(x) x = self.proj(x[:, 0, :]) return xsummary(VisionTransformer(),input_size=(16, 3, 224, 224))will get:
=============================================================================================== Layer (type:depth-idx) Output Shape Param # =============================================================================================== VisionTransformer [16, 1000] 151,296 ├─PatchEmbedding: 1-1 [16, 196, 768] -- │ └─Conv2d: 2-1 [16, 768, 14, 14] 590,592 ├─TransformerEncoder: 1-2 [16, 197, 768] -- │ └─ModuleList: 2-2 -- -- │ │ └─TransformerEncoderLayer: 3-1 [16, 197, 768] 7,087,872 │ │ └─TransformerEncoderLayer: 3-2 [16, 197, 768] 7,087,872 │ │ └─TransformerEncoderLayer: 3-3 [16, 197, 768] 7,087,872 │ │ └─TransformerEncoderLayer: 3-4 [16, 197, 768] 7,087,872 │ │ └─TransformerEncoderLayer: 3-5 [16, 197, 768] 7,087,872 │ │ └─TransformerEncoderLayer: 3-6 [16, 197, 768] 7,087,872 │ │ └─TransformerEncoderLayer: 3-7 [16, 197, 768] 7,087,872 │ │ └─TransformerEncoderLayer: 3-8 [16, 197, 768] 7,087,872 │ │ └─TransformerEncoderLayer: 3-9 [16, 197, 768] 7,087,872 │ │ └─TransformerEncoderLayer: 3-10 [16, 197, 768] 7,087,872 │ │ └─TransformerEncoderLayer: 3-11 [16, 197, 768] 7,087,872 │ │ └─TransformerEncoderLayer: 3-12 [16, 197, 768] 7,087,872 ├─Linear: 1-3 [16, 1000] 769,000 =============================================================================================== Total params: 86,565,352 Trainable params: 86,565,352 Non-trainable params: 0 Total mult-adds (G): 3.23 =============================================================================================== Input size (MB): 9.63 Forward/backward pass size (MB): 2575.69 Params size (MB): 345.66 Estimated Total Size (MB): 2930.98 ===============================================================================================nn.TransformerEncoder(torch 2.2.0+cu121)class VisionTransformer_torch(nn.Module): def __init__( self, image_size=224, in_channels=3, patch_size=16, num_classes=1000, num_layers=12, num_heads=12, hidden_dim=768, ffn_dim=3072, dropout=0.0 ): super().__init__() self.patch_embedding = PatchEmbedding(in_channels, patch_size, hidden_dim) self.pos_embedding = nn.Parameter(torch.empty(1, (image_size // patch_size)**2, hidden_dim).normal_(std=0.02)) self.class_token = nn.Parameter(torch.empty(1, 1, hidden_dim)) transformer_encoder_layer = nn.TransformerEncoderLayer(d_model=hidden_dim, nhead=num_heads, dim_feedforward=ffn_dim, dropout=dropout, batch_first=True) self.transformer_encoder = nn.TransformerEncoder(transformer_encoder_layer, num_layers=num_layers) # self.layer_norm = nn.LayerNorm(hidden_dim) self.proj = nn.Linear(hidden_dim, num_classes) def forward(self, x): x = self.patch_embedding(x) x += self.pos_embedding batch_size = x.shape[0] batch_class_token = self.class_token.expand(batch_size, -1, -1) x = torch.cat([batch_class_token, x], dim=1) x = self.transformer_encoder(x) # x = self.layer_norm(x) x = self.proj(x[:, 0, :]) return xsummary(VisionTransformer_torch(),input_size=(16, 3, 224, 224))will, surprisingly, get the same total parameters (
86,565,352), though the sizes (MB) are way smaller:=============================================================================================== Layer (type:depth-idx) Output Shape Param # =============================================================================================== VisionTransformer_torch [16, 1000] 151,296 ├─PatchEmbedding: 1-1 [16, 196, 768] -- │ └─Conv2d: 2-1 [16, 768, 14, 14] 590,592 ├─TransformerEncoder: 1-2 [16, 197, 768] -- │ └─ModuleList: 2-2 -- -- │ │ └─TransformerEncoderLayer: 3-1 [16, 197, 768] 7,087,872 │ │ └─TransformerEncoderLayer: 3-2 [16, 197, 768] 7,087,872 │ │ └─TransformerEncoderLayer: 3-3 [16, 197, 768] 7,087,872 │ │ └─TransformerEncoderLayer: 3-4 [16, 197, 768] 7,087,872 │ │ └─TransformerEncoderLayer: 3-5 [16, 197, 768] 7,087,872 │ │ └─TransformerEncoderLayer: 3-6 [16, 197, 768] 7,087,872 │ │ └─TransformerEncoderLayer: 3-7 [16, 197, 768] 7,087,872 │ │ └─TransformerEncoderLayer: 3-8 [16, 197, 768] 7,087,872 │ │ └─TransformerEncoderLayer: 3-9 [16, 197, 768] 7,087,872 │ │ └─TransformerEncoderLayer: 3-10 [16, 197, 768] 7,087,872 │ │ └─TransformerEncoderLayer: 3-11 [16, 197, 768] 7,087,872 │ │ └─TransformerEncoderLayer: 3-12 [16, 197, 768] 7,087,872 ├─Linear: 1-3 [16, 1000] 769,000 =============================================================================================== Total params: 86,565,352 Trainable params: 86,565,352 Non-trainable params: 0 Total mult-adds (G): 1.86 =============================================================================================== Input size (MB): 9.63 Forward/backward pass size (MB): 19.40 Params size (MB): 5.44 Estimated Total Size (MB): 34.47 ===============================================================================================
§3.5.3 fine-tuning of ViT
[2203.09795] Three things everyone should know about Vision Transformers:
- Parallel vision transformers.
- Fine-tuning attention is all you need.
- Patch preprocessing with masked self-supervised learning.
§3.6 Generative Pre-trained Transformer (GPT)
Note that in the original Transformer, the Decoder has two attention. However in the Decoder of GPT, there is only one attention. And GPTs are called “Decoder-Only” because:
- By using masks, GPTs are autoregressive, meaning that the model takes previous $(t-1)^{th}$ words to produce the $t^{th}$ word.
- Their task is to generate text, similar to the Decoder in the original Transformer.
§3.6.1 GPTDecoderLayer
class GPTDecoderLayer(nn.Module):
def __init__(self, num_layers=12, num_heads=12, hidden_dim=768, ffn_dim=3072, dropout=0.0):
super().__init__()
self.layer_norm_1 = nn.LayerNorm(hidden_dim)
self.attention = MultiheadAttention(hidden_dim, num_heads, dropout)
self.layer_norm_2 = nn.LayerNorm(hidden_dim)
self.ffn = FFN(hidden_dim, ffn_dim, hidden_dim, dropout)
self.dropout = nn.Dropout(dropout)
self.attn_scale = 1 / math.sqrt(2 * num_layersr)
def forward(self, x, is_causal=True):
residual = x
x = self.layer_norm_1(x)
x = self.attn_scale * self.attention(x, is_causal)
x = self.dropout(x)
x += residual
residual = x
x = self.layer_norm_2(x)
x = self.ffn(x)
x = self.dropout(x)
x += residual
return x
§3.6.2 GPTDecoder
class GPTDecoder(nn.Module):
def __init__(self, num_layers=12, num_heads=12, hidden_dim=768, ffn_dim=3072, dropout=0.0):
super().__init__()
self.gpt_decoder_layers = nn.ModuleList([
GPTDecoderLayer(num_layers, num_heads, hidden_dim, ffn_dim, dropout)
for _ in range(num_layers)
])
def forward(self, x, is_causal=True):
for gpt_decoder_layer in self.gpt_decoder_layers:
x = gpt_decoder_layer(x, is_causal)
return x
§3.6.3 GPTLanguageModel
class GPTLanguageModel(nn.Module):
def __init__(
self, vocab_size=50257, window_size=1024,
num_layers=12, num_heads=12, hidden_dim=768, ffn_dim=3072, dropout=0.0
):
super().__init__()
self.embedding = Embedding(hidden_dim, vocab_size)
self.positional_encoding = PositionalEncoding(hidden_dim, vocab_size, dropout)
self.gpt_decoder = GPTDecoder(num_layers, num_heads, hidden_dim, ffn_dim, dropout)
self.layer_norm = nn.LayerNorm(hidden_dim)
self.proj = nn.Linear(hidden_dim, vocab_size, bias=False)
self.proj.weight = self.embedding.weight# https://arxiv.org/abs/1608.05859
def forward(self, index, targets=None):
# index, targets shape: [batch_size, seq_length]
batch_size, seq_length = index.shape
# embedding
x = self.embedding(index)# [batch_size, seq_length, hidden_dim]
x = self.positional_encoding(x)# [batch_size, seq_length, hidden_dim]
# Transformer Decoder
x = self.gpt_decoder(x)# [batch_size, seq_length, hidden_dim]
# project out
x = self.layer_norm(x)# [batch_size, seq_length, hidden_dim]
logits = self.proj(x)# [batch_size, seq_length, vocab_size]
if targets is None:
loss = None
else:
batch_size, seq_length, vocab_size = logits.shape
logits = logits.view(batch_size*seq_length, vocab_size)
targets = targets.view(batch_size*seq_length)
loss = F.cross_entropy(logits, targets)
return logits, loss
@torch.no_grad()
def generate(self, index, max_new_tokens):
# index shape [batch_size, seq_length]
for _ in range(max_new_tokens):
# crop index to the last window_size tokens
index_cond = index[:, -window_size:]
# get the predictions
logits, loss = self(index_cond)
# focus only on the last time step
logits = logits[:, -1, :] # [batch_size, vocab_size]
# apply softmax to get probabilities
probs = F.softmax(logits, dim=-1) # [batch_size, vocab_size]
# sample from the distribution
index_next = torch.multinomial(probs, num_samples=1) # [batch_size, 1]
# append sampled index to the running sequence
index = torch.cat((index, index_next), dim=1) # [batch_size, seq_length+1]
return index
gpt_language_model = GPTLanguageModel()
index = torch.randint(50257, (1, 196))# [batch_size, seq_length]
targets = torch.randint(50257, (1, 196))# [batch_size, seq_length]
logits, loss = gpt_language_model(index, targets)
print(logits.shape)# [batch_size*seq_length, vocab_size]
print(loss)
will get:
torch.Size([196, 50257])
tensor(10.9951, grad_fn=<NllLossBackward0>)
§3.6.4 fine-tuning of LLM
The ULMFiT 3-step approach (see Fig.1 of [1801.06146] Universal Language Model Fine-tuning for Text Classification):
- Language Model pre-training.
- Instruction tuning.
- RLHF (Reinforcement Learning from Human Feedback).
§3.7 Variants
Generally speaking most papers have this kind of naming convention:
- Original Transformer: 1706.03762
- Vanilla Transformer: The original Transformer with ReLU activation and layer normalization 1607.06450 outside of the residual path.
- Transformer+GELU: A variant of the vanilla Transformer that uses GELU 1606.08415 activations or its approximation.
- Transformer++: A variant of the vanilla Transformer that uses RMS normalization 1910.07467, Swish activation 1710.05941 and GLU multiplicative branch 1612.08083 in the FFN (SwiGLU) 2002.05202.
§3.8 Mixture of Experts (MoE)
Mixture of Experts (MoE): | [1701.06538] Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer | mixture-of-experts (GitHub) | st-moe-pytorch (GitHub) | FastMoE (GitHub) | Training MoEs at Scale with PyTorch |
Mixtral of Experts: | [2401.04088] Mixtral of Experts | mistral-src (GitHub) |
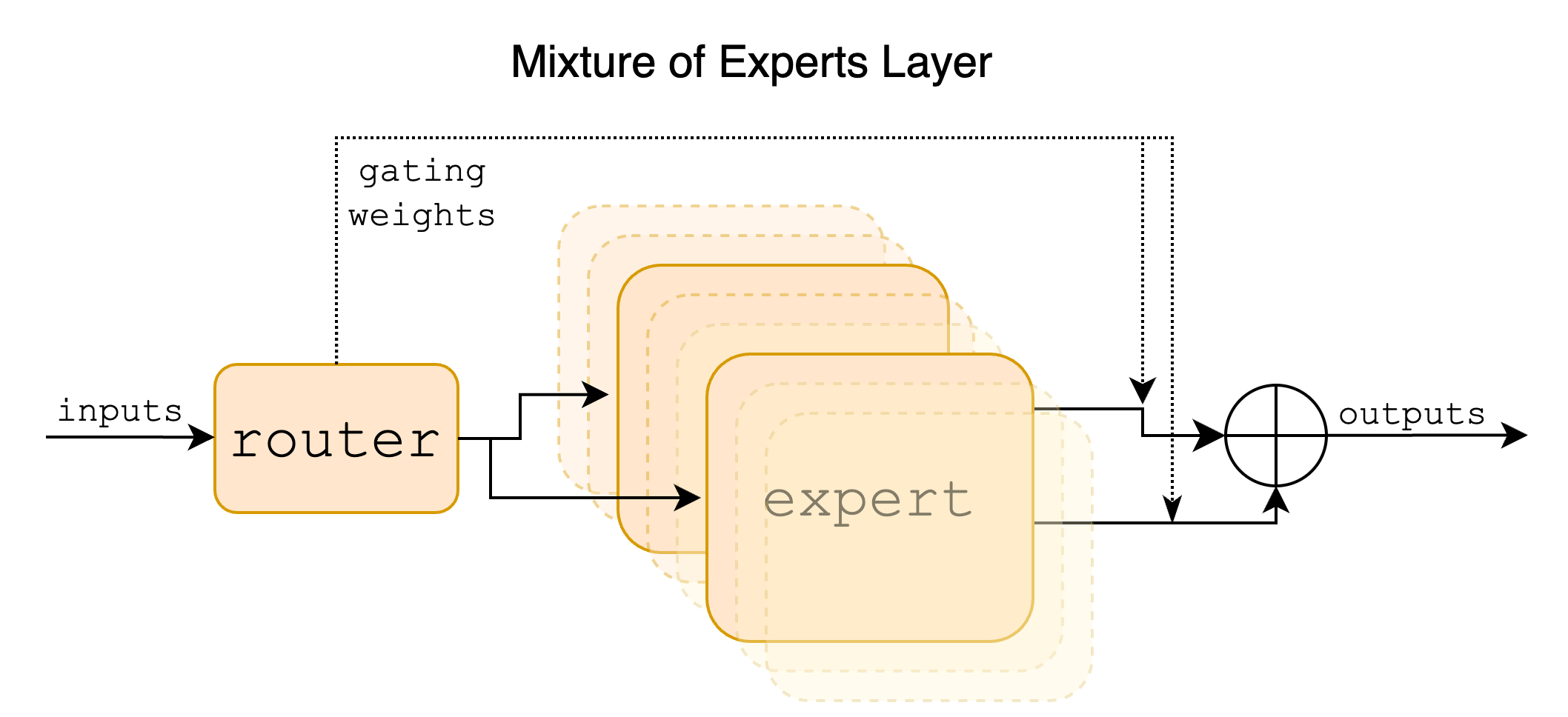
FFN in the original Transformer is replaced by Mixture of Expert layer (weighted FFNs). Given $n$ experts $\lbrace{E_0, E_i, …, E_{n-1}}\rbrace$, the output of the MoE is$$\text{MoE}(x) = \sum_{i=0}^{n-1} {G(x)}_{i} \cdot E_i(x)$$where $$G(x) = \text{Softmax}(\text{TopK}(x W_g))$$By using torch.topk, we only uses $K$ Experts, thus this model is also called Sparse Mixture of Experts (SMoE). Another benefit of experts is that we can put different experts on different GPUs, which is the similar approach of AlexNet. (It is rumored that GPT4 is using 16 experts with top2 gating. I guess Ilya Sutskever pulled the same trick again.) This usage of $\text{TopK}$ is similar to Beam Search for inferencing.
In Mixtral of Experts, $E(x)$ is SwiGLU FFN: $$\text{FFN}_\text{SwiGLU}(x) = (\text{Swish}_1(xW_1) \odot xV)W_2$$here we use F.silu.
class FFN_SwiGLU(nn.Module):
def __init__(self, hidden_dim=4096, ffn_dim=14336):
super().__init__()
self.w1 = nn.Linear(hidden_dim, ffn_dim, bias=False)
self.v = nn.Linear(hidden_dim, ffn_dim, bias=False)
self.w2 = nn.Linear(ffn_dim, hidden_dim, bias=False)
def forward(self, x):
return self.w2(F.silu(self.w1(x)) * self.v(x))
# https://github.com/pytorch/torchtitan/blob/main/torchtitan/models/llama/model.py#L250
# https://github.com/pytorch/torchtitan/blob/main/torchtitan/models/llama/model.py#L300
def init_weights(self, init_std):
nn.init.trunc_normal_(self.w1.weight, mean=0.0, std=0.02)
nn.init.trunc_normal_(self.v.weight, mean=0.0, std=init_std)
nn.init.trunc_normal_(self.w2.weight, mean=0.0, std=init_std)
class MoELayer(nn.Module):
def __init__(self, hidden_dim=4096, ffn_dim=14336, num_experts=8, num_experts_per_tok=2):
super().__init__()
self.experts = nn.ModuleList([
FFN_SwiGLU(hidden_dim, ffn_dim)
for _ in range(num_experts)
])
self.gate = nn.Linear(hidden_dim, num_experts, bias=False)
self.num_experts_per_tok = num_experts_per_tok
def forward(self, inputs):
inputs_squashed = inputs.view(-1, inputs.shape[-1])# [batch_size * seq_length, hidden_dim]
gate_logits = self.gate(inputs_squashed)# [batch_size * seq_length, num_experts]
weights, selected_experts = torch.topk(gate_logits, self.num_experts_per_tok)# both [batch_size * seq_length, num_experts_per_tok]
# print(selected_experts)
weights = F.softmax(weights, dim=1)
# iterate over each expert
results = torch.zeros_like(inputs_squashed)
for i, expert in enumerate(self.experts):
(index, nth_expert) = torch.where(selected_experts == i)# both [num_index], num_index ≤ batch_size * seq_length
# print(torch.where(selected_experts == i))
results[index] += weights[index, nth_expert, None] * expert(inputs_squashed[index])# [num_index, 1] * [num_index, hidden_dim]
results = results.view_as(inputs)
return results
moe_layer = MoELayer(hidden_dim=8, ffn_dim=16)
dummy = torch.rand(1, 3, 8)# [batch_size, seq_length, hidden_dim]
dummy = moe_layer(dummy)# [batch_size, seq_length, hidden_dim]
will get:
tensor([[7, 3],
[7, 0],
[7, 0]])
(tensor([1, 2]), tensor([1, 1]))
(tensor([], dtype=torch.int64), tensor([], dtype=torch.int64))
(tensor([], dtype=torch.int64), tensor([], dtype=torch.int64))
(tensor([0]), tensor([1]))
(tensor([], dtype=torch.int64), tensor([], dtype=torch.int64))
(tensor([], dtype=torch.int64), tensor([], dtype=torch.int64))
(tensor([], dtype=torch.int64), tensor([], dtype=torch.int64))
(tensor([0, 1, 2]), tensor([0, 0, 0]))
There is a similar architecture called MoD (Mixture of Depth), where certain Transformer blocks are skipped by some gated mechanism. Below is Fig.1 of [2404.02258] Mixture-of-Depths: Dynamically allocating compute in transformer-based language models:
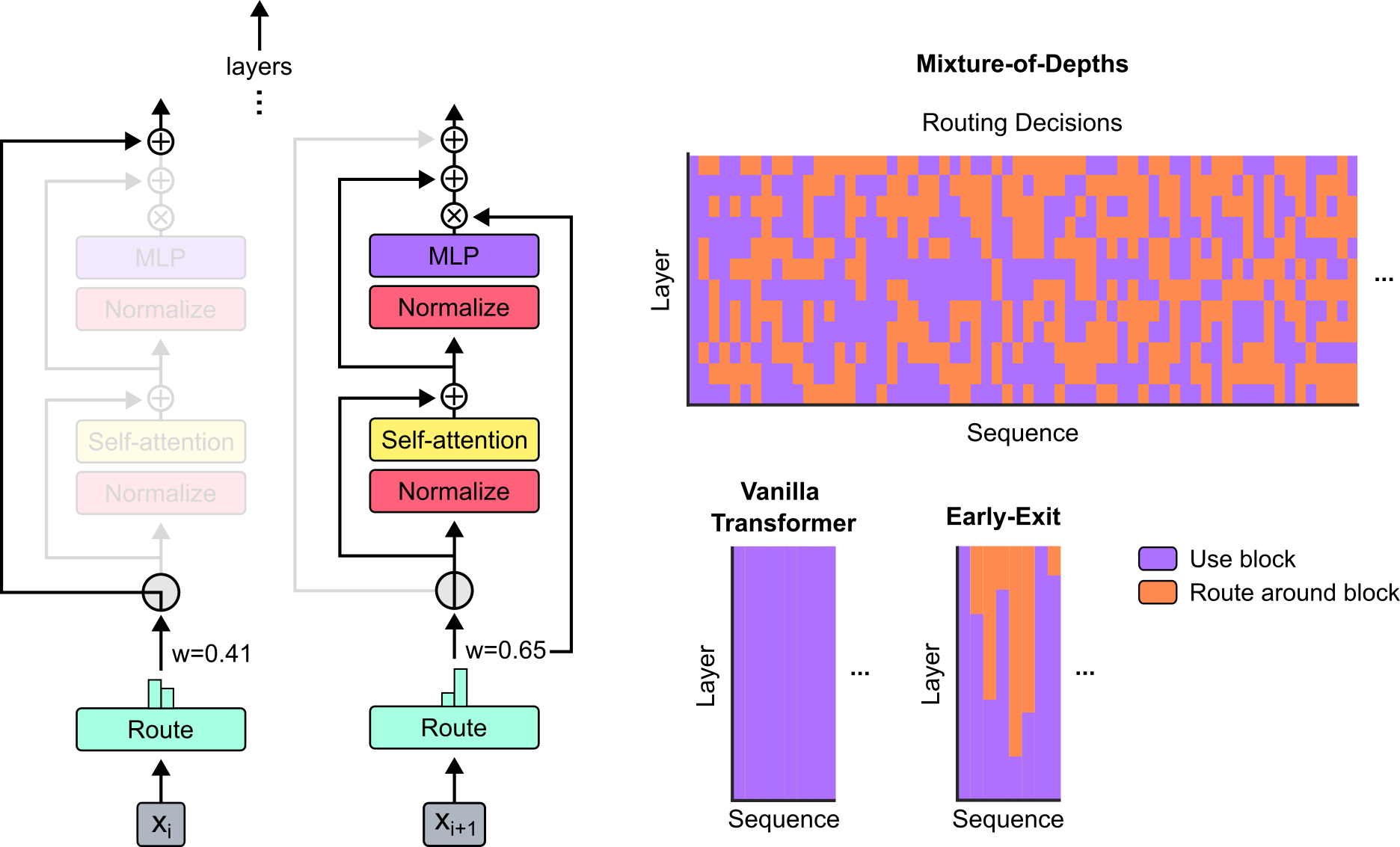
Naturally, Route is a nn.Linear. I find this post explaining the technical difficulty we have with this architecture really well.
[2407.09298] Transformer Layers as Painters does a lot of experiments on removing or sharing layers in Transformer:
1.There are three distinct classes of layers (with Middle being the largest). 2. The middle layers have some degree of uniformity (but not redundancy). And 3. Execution order matters more for math and reasoning tasks than semantic tasks.
§3.9 Scaling Laws, Emergence
| [2010.14701] Scaling Laws for Autoregressive Generative Modeling | [2203.15556] Training Compute-Optimal Large Language Models | [2304.01373] Pythia: A Suite for Analyzing Large Language Models Across Training and Scaling |
Previously in this article it is stated that Transformer is a general function fitter, one of the reasons is that Transformers follow scaling laws with fitting line being almost perfect.
Below is Fig.1 of [2010.14701] Scaling Laws for Autoregressive Generative Modeling. As we can see, the line of power law can be fitted almost perfectly. And every time I look at it I’m amazed, you don’t see this kind of smoothness in other NNs. RNN, for example, is really hard to train.

The effect of scaling law can sometimes be misunderstood as emergence, see Emergent abilities and grokking: Fundamental, Mirage, or both? – Windows On Theory. I especially enjoy the “jumping over a 1-meter hurdle” analogue. Metrics of LLMs can be tricky.
§3.10 Transformers are CNNs, RNNs, GNNs
Another reason that Transformers are general function fitter is that: CNNs assume invariance of space transformation (adjacent pixels are related); RNNs assume the continuity of time series (adjacent words are related); GNNs assume the preservation of graph symmetry (a graph can be rearranged or mapped onto itself while preserving the configuration of its connections); and Transformers do not have these initial bias.
At the end of the day, we are transforming [batch_size, seq_length, hidden_dim] to [batch_size, seq_length, hidden_dim]. The intermediate steps are not important, or we happen to have found the general function fitter that is good enough for most tasks: Transformer, as I mentioned in the beginning of this chapter. See The Bitter Lesson.
§4 fastai
| fastai (GitHub) | fastai (docs) | Practical Deep Learning |
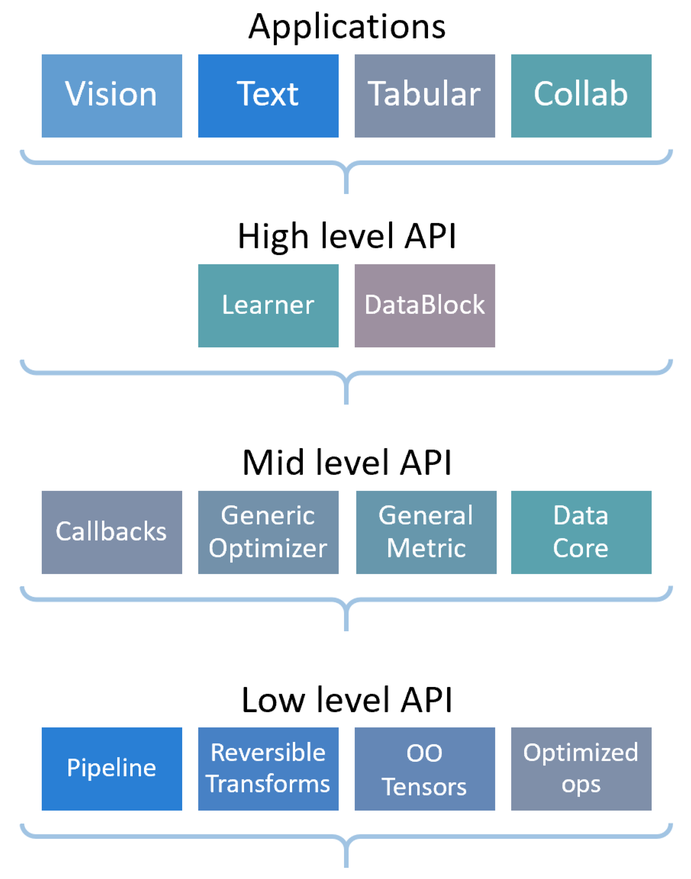
§4.1 Dataloaders
We did not write Datasets & DataLoaders, because it’s highly variable from tasks to tasks. In general I would suggest:
- Let your brain (bio-neural networks) understand the dataset intuitively by visualizing lots of examples from the dataset. (See A Recipe for Training Neural Networks)
- Use
polars,mojoto load data because it’s faster and more memory saving.
from torch.utils.data import Dataset, DataLoader, SequentialSampler, BatchSampler
from fastai.vision.all import *
# subclass `torch.utils.data.Dataset` to create a custom Dataset
class MyDataset(Dataset):
def __init__(self):
...
def __len__(self):
...
def __getitem__(self, index):
...
return image, label# shape: image is [C, H, W], label is []
# use `torch.utils.data` to load data
dataset = MyDataset()
data_size = len(dataset)
train_size = int(0.8 * data_size)# 80% is train_loader
indices = list(range(data_size))
train_indices = indices[:train_size]
train_batch_sampler = BatchSampler(SequentialSampler(train_indices),batch_size=32,drop_last=False)
train_loader = DataLoader(dataset,num_workers=4,batch_sampler=train_batch_sampler)
val_indices = indices[train_size:]
val_batch_sampler = BatchSampler(SequentialSampler(val_indices),batch_size=32,drop_last=False)
val_loader = DataLoader(dataset,num_workers=1,batch_sampler=val_batch_sampler)
# use `fastai.vision.all.DataLoaders` to combine training data and validation data
dls = DataLoaders(train_loader, val_loader)
Or you can use DataBlock.
§4.2 Learner
Load the model:
model = MyModel().cuda()
Use fastai.vision.all.OptimWrapper to wrap AdamW optimizer:
def WrapperAdamW(param_groups,**kwargs):
return OptimWrapper(param_groups,torch.optim.AdamW)
Learner, Learner.to_fp16, Callbacks:
from functools import partial# python standard library
learn = Learner(
dls,
model,
path='custom_path',
loss_func=custom_loss,
metrics=[custom_metric],
opt_func=partial(WrapperAdamW,eps=1e-7),
# opt_func=partial(OptimWrapper,opt=torch.optim.AdamW,eps=1e-7)
cbs=[
CSVLogger(),
GradientClip(3.0),
EMACallback(),
SaveModelCallback(monitor='custom_metric',comp=np.less,every_epoch=True),
GradientAccumulation(n_acc=4096//32)# divided by `batch_size`
]
).to_fp16()
Learner.lr_find, [1506.01186] Cyclical Learning Rates for Training Neural Networks:
learn.lr_find(suggest_funcs=(slide, valley))
Learner.fit_one_cycle uses 1cycle policy:
learn.fit_one_cycle(
8,
lr_max=1e-5,
wd=0.05,
pct_start=0.25,
div=25,
div_final=100000,
)
learn.save("my_model_opt", with_opt=True)
learn.save("my_model", with_opt=False)
Learner.compile, torch.compile:
from fastxtend.callback import compiler
Learner(...).compile()
# or
Learner(..., cbs=CompilerCallback())
§5 Transfer Learning
For different dataset and different goals.
§5.1 Load Pretrained ResNet, ViT
| Which Timm Models Are Best 2023-11-29 | Kaggle |
ResNet101fastai.vision.all.vision_learnerfrom fastai.vision.all import * # https://github.com/pytorch/vision/tree/main/torchvision/models from torchvision.models import resnet101 # https://pytorch.org/vision/stable/models.html from torchvision.models import ResNet101_Weights dls = ... learn = vision_learner( dls, resnet101, pretrained=True, weights=ResNet101_Weights.IMAGENET1K_V2, metrics=error_rate ) learn.fine_tune( freeze_epochs=1,# freeze_epochs run first epochs=3, ) learn.save("finetuned_resnet101", with_opt=False)ViT_B_16from fastai.vision.all import * from torchvision.models import vit_b_16 from torchvision.models import ViT_B_16_Weights dls = ... # https://github.com/rasbt/ViT-finetuning-scripts/ model = vit_b_16(weights=ViT_B_16_Weights.IMAGENET1K_V1) model.heads.head = nn.Linear(in_features=768, out_features=2)# replace projection layer model.to("cuda") learn = Learner(dls, model, metrics=error_rate) learn.fine_tune(freeze_epochs=1, epochs=3) learn.save("finetuned_vit_b_16", with_opt=False)
§5.2 Acoustic/Gravitational Wave Classification
[1912.11370] Big Transfer (BiT): General Visual Representation Learning:
We scale up pre-training, and propose a simple recipe that we call Big Transfer (BiT).
§5.2.1 Acoustic Wave Classification
- Great results on audio classification with fastai library | by Ethan Sutin
UrbanSoundClassification.ipynb(GitHub)
Each subfigure of the figure below is a Power Spectrum:
- The horizontal axis is Time ($\text{s}$).
- The vertical axis is Frequency ($\text{Hz}$) of the vibration.
- The color (from dark to red to white) is Sound Intensity Level ($\text{dB}$):
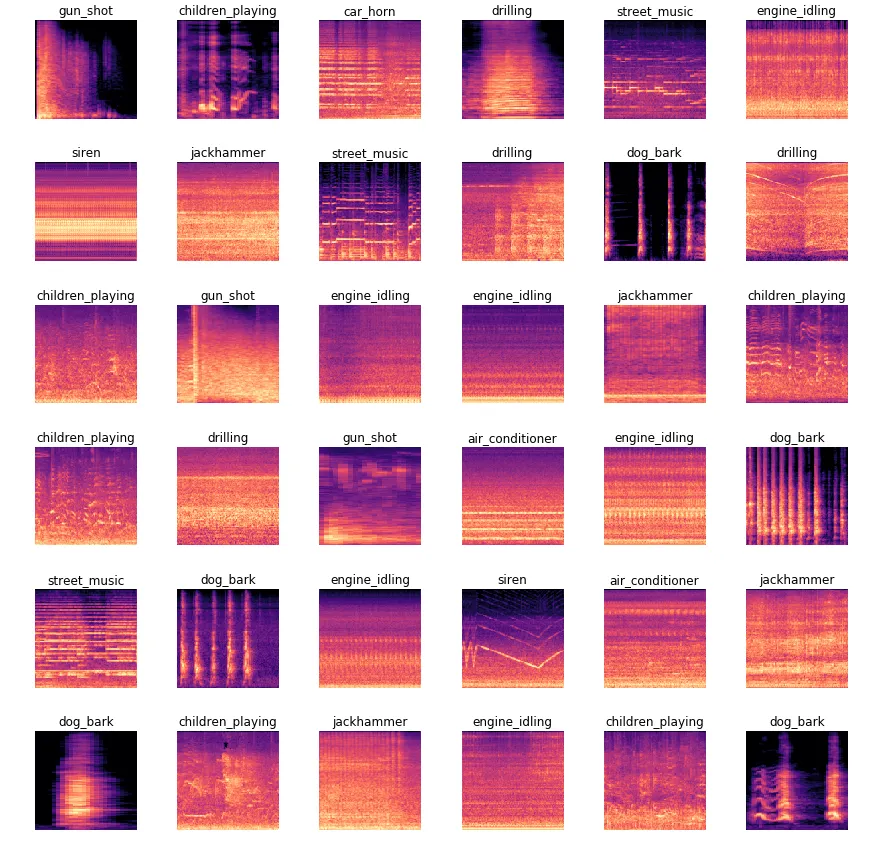
Use librosa.display.specshow to draw Power Spectrum, then save as .png:
S = librosa.feature.melspectrogram(y=samples, sr=sample_rate)
librosa.display.specshow(librosa.power_to_db(S, ref=np.max))
filename = spectrogram_path/fold/Path(audio_file).name.replace('.wav','.png')
plt.savefig(filename, dpi=400, bbox_inches='tight',pad_inches=0)
Use fastai to load pretrained model ResNet34:
learn = cnn_learner(data, models.resnet34, metrics=error_rate)
§5.2.2 Gravitational Wave Classification
The picture below is Fig.2 of the paper:

Use fastai to load pretrained model ResNet18, ResNet26, ResNet34, ResNet50, ConvNext_Nano, ConvNext_Tiny.
§5.3 Category “Unknown”, Confidence Level
- Choose the size of the model by the size of the dataset, to avoid overfitting.
- When the output probability of the final MLP layer is not dominated by one category (less than 95% or some threshold), you should be extra careful. Because actually this prediction is not correct. There is an entire research field on predicting the confidence level of a prediction, see [2103.15718] von Mises-Fisher Loss: An Exploration of Embedding Geometries for Supervised Learning, [2107.03342] A Survey of Uncertainty in Deep Neural Networks, [1706.04599] On Calibration of Modern Neural Networks.
